面对全球金融危机的挑战，我国政府毅然启动内需，改善民生．国务院决定从2009年2月1日起，“家电下乡”在全国范围内实施，农民购买人选产品，政府按原价购买总额的13%给予补贴返还．某村委会组织部分农民到商场购买人选的同一型号的冰箱、电视机两种家电，已知购买冰箱的数量是电视机的2倍，且按原价购买冰箱总额为40000元、电视机总额为15000元．根据“家电下乡”优惠政策，每台冰箱补贴返还的金额比每台电视机补贴返还的金额多65元，求冰箱、电视机各购买多少台？
（1）设购买电视机
台，依题意填充下列表格：
 项目家电种类 |
购买数量（台） |
原价购买总额（元） |
政府补贴返还比例 |
补贴返还总金额（元） |
每台补贴返还金额（元） |
| 冰箱 |
|
40 000 |
13% |
|
|
| 电视机 |
|
15 000 |
13% |
|
|
（2）列出方程（组）并解答．
如图：已知正方形ABCD的对角线AC长为20cm，半径为1的⊙O1的圆心O1从A点出发以1cm/s的速度向C运动，半径为1的⊙O2的圆心O2从C点出发以2cm/s的速度向A运动且半径同时也以1cm/s的速度不断增大，两圆同时运动，当其中一个圆的圆心运动到AC的端点时，另一个圆也停止运动．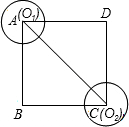
（1）当O1运动了几秒时，⊙O1与AD相切？
（2）当O2运动了几秒时，⊙O2与CB相切？
（3）当O2运动了几秒时，⊙O1与⊙O2相切？
矩形ABCD中，AD=5，AB=3，将矩形ABCD沿某直线折叠，使点A的对应点A′落在线段BC上，再打开得到折痕EF．
（1）当A′与B重合时（如图1），EF=；当折痕EF过点D时（如图2），求线段EF的长；
（2）观察图3和图4，设BA′=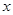
，①当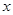的取值范围是时，四边形AEA′F是菱形；②在①的条件下，利用图4证明四边形AEA′F是菱形．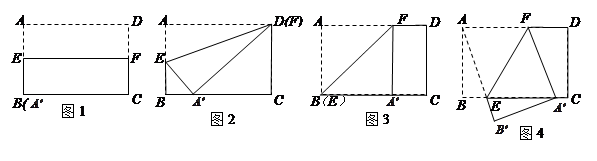
已知关于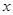
的一元二次方程
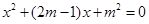有两个实数根
和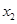
．
（1）求实数
的取值范围；（2）当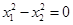
时，求的值．
如图，将□ABCD的边DC延长到点E，使CE＝DC，连接AE，交BC于点F．⑴求证：△ABF≌△ECF
⑵若∠AFC＝2∠D，连接AC、BE．求证：四边形ABEC是矩形．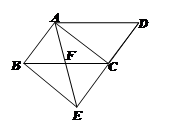
已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．
(1)求抛物线的解析式和对称轴；
(2)设点P是直线l上的一个动点，当△PAC是以AC为斜边的Rt△时，求点P的坐标；
(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由；
(4)设过点A的直线与抛物线在第一象限的交点为N，当△ACN的面积为
时，求直线AN的解析式.