从某电视塔塔顶附近的平台处释放一个小球,不计空气阻力和风的作用,小球自由下落。若小球在落地前的最后2s内的位移是80m,求:
(1)该平台离地面的高度。
(2)该小球落地时的瞬时速度大小。(取g=10m/s2)
【改编】下图是某装置的垂直截面图,虚线A1A2是垂直截面与磁场区边界面的交线,匀强磁场分布在A1A2的右侧区域,磁感应强度B=0.4T,方向垂直纸面向外,A1A2与垂直截面上的水平线夹角为45°。A1A2的左侧,固定的薄板和等大的挡板均水平放置,它们与垂直截面交线分别为S1、S2,相距L=0.2m。在薄板上P处开一小孔,P与A1A2线上点D的水平距离为L。在小孔处装一个电子快门。起初快门开启,一旦有带正电微粒通过小孔,快门立即关闭,此后每隔T=3.0×10-3s开启一次并瞬间关闭。从S1S2之间的某一位置水平发射一速度为v0的带正电微粒,它经过磁场区域后入射到P处小孔。通过小孔的微粒与档板发生碰撞而反弹,反弹速度大小是碰前的0.5倍。(忽略微粒所受重力影响,碰撞过程无电荷转移。已知微粒的荷质比 。只考虑纸面上带电微粒的运动)求:
。只考虑纸面上带电微粒的运动)求:
(1)满足题目的微粒在磁场中运动的半径的条件?
(2)经过一次反弹直接从小孔射出的微粒,其初速度v0应为多少?
(3)上述(2)问中微粒从最初水平射入磁场的位置到D点的距离d1和第二次离开磁场的位置到D点的距离d2。
如图所示,一个长度为L=1m、高度为h=0.8m的长木板静止在水平地面上,其质量M=0.4kg,一质量m=0.1kg的小物块(可视为质点)放置在其上表面的最右端.物块与长木板,长木板与地面之间动摩擦因数均为μ=0.5.设最大静摩擦力等于滑动摩擦力.现给长木板施加一个水平向右持续作用的外力F.
(1)若F恒为4 N,试求长木板的加速度大小;
(2)若F恒为5.8 N,试判断物块是否能从长木板上掉下,如能,请求出小物块落地时距长木板左端的距离;如不能,求出物块距长木板右端的距离;
(3)若F=kt,k>0,在t=0时刻到物块刚滑落时间内,试定性画出物块与长木板间摩擦力大小随时间变化的图线,无需标注时间以及力的大小.
工厂里有一种运货的过程可以简化为如图所示,货物以 的初速度滑上静止的货车的左端,已知货物质量m=20kg,货车质量M=30kg,货车高h=0.8m。在光滑轨道OB上的A点设置一固定的障碍物,当货车撞到障碍物时会被粘住不动,而货物就被抛出,恰好会沿BC方向落在B点。已知货车上表面的动摩擦因数
的初速度滑上静止的货车的左端,已知货物质量m=20kg,货车质量M=30kg,货车高h=0.8m。在光滑轨道OB上的A点设置一固定的障碍物,当货车撞到障碍物时会被粘住不动,而货物就被抛出,恰好会沿BC方向落在B点。已知货车上表面的动摩擦因数 ,货物可简化为质点,斜面的倾角为
,货物可简化为质点,斜面的倾角为 。
。
①求货物从A点到B点的时间;
②求AB之间的水平距离;
③若已知OA段距离足够长,导致货物在碰到A之前已经与货车达到共同速度,则货车的长度是多少?
如图所示,AOBC为某种透明介质的截面图,其中△AOC为直角三角形,∠OAC=53°.BC为半径R=16cm的四分之一圆弧,AB与水平屏幕MN垂直并接触于A点.由红光和紫光两种单色光组成的复色光射向圆心O,在AB分界面上的入射角i=53°,结果在水平屏幕MN上出现两个亮斑.已知该介质对红光和紫光的折射率分别为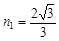 ,
,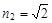 ,sin53°=0.8;cos53°=0.6.
,sin53°=0.8;cos53°=0.6.
①判断在AM和AN两处产生亮斑的颜色;
②求两个亮斑间的距离.
).(如图,一导热性能良好、内壁光滑的气缸水平放置,横截面积S=1.0×l0-3m2、质量m=2kg、厚度不计的活塞与气缸底部之间封闭了一部分理想气体,此时活塞与气缸底部之间的距离l=36cm,在活塞的右侧距离其d=14cm处有一对与气缸固定连接的卡环。气体的温度t=27℃,外界大气压强p0=l.0×105Pa。现将气缸开口向上竖直放置 (g取10m/s2)
①求此时活塞与气缸底部之间的距离h;
②如果将缸内气体加热到600K,求此时气体的压强p。