(本小题满分15分)
若函数f(x)=ax3+bx2+cx+d是奇函数,且f(x)极小值=f(-)=-.
(1)求函数f(x)的解析式;
(2)求函数f(x)在[-1,m](m>-1)上的最大值;
(3)设函数g(x)=,若不等式g(x)·g(2k-x)≥(-k)2在(0,2k)上恒成立,求实数k的取值范围.
(本小题满分12分)某运动队拟在2015年3月份安排5次体能测试,规定:依次测试,只需有一次测试合格就不必参加后续的测试.已知运动员小刘5次测试每次合格的概率依次构成一个公差为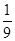 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过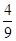 ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为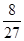 .
.
(Ⅰ)求小刘第一次参加测试就合格的概率;
(Ⅱ)在小刘参加第一、第二次测试均不合格的前提下,记小刘参加后续测试的次数为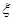 ,求随机变量
,求随机变量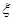 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知函数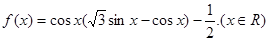
(Ⅰ)求函数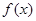 的对称中心;
的对称中心;
(Ⅱ)已知△ABC内角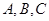 的对边分别为
的对边分别为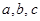 ,且
,且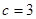 ,
,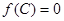 ,
,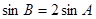 ,求
,求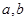
(本小题满分14分)设函数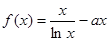 .
.
(1)若函数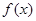 在
在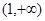 上为减函数,求实数
上为减函数,求实数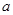 的最小值;
的最小值;
(2)若存在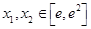 ,使
,使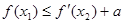 成立,求实数
成立,求实数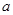 的取值范围.
的取值范围.
(本小题满分13分)已知椭圆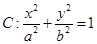 (
(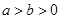 )的左、右顶点分别为
)的左、右顶点分别为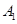 ,
, ,且
,且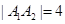 ,
,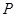 为椭圆上异于
为椭圆上异于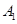 ,
, 的点,
的点,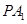 和
和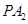 的斜率之积为
的斜率之积为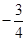 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设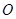 为椭圆中心,
为椭圆中心,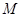 ,
,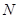 是椭圆上异于顶点的两个动点,求
是椭圆上异于顶点的两个动点,求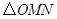 面积的最大值.
面积的最大值.
(本小题满分12分)已知单调递增的等比数列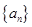 满足:
满足: ,且
,且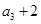 是
是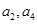 的等差中项.
的等差中项.
(Ⅰ)求数列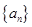 的通项公式;
的通项公式;
(Ⅱ)若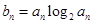 ,
,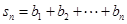 ,求
,求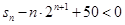 成立的正整数
成立的正整数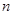 的最小值.
的最小值.