若对任意x∈R，y∈R有唯一确定的f (x，y)与之对应，则称f (x，y)为关于x，y的二元函数．定义：同时满足下列性质的二元函数f (x，y)为关于实数x，y的广义“距离”：
（Ⅰ）非负性：f (x，y)≥0；
（Ⅱ）对称性：f (x，y)= f (y，x)；
（Ⅲ）三角形不等式：f (x，y)≤f (x，z)+ f (z，y)对任意的实数z均成立．
给出下列二元函数：
①f (x，y)=(x-y)2；②f (x，y)=|x-y|；③f (x，y)=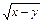
；④f (x，y)=|sin(x-y)|．
则其中能够成为关于x，y的广义“距离”的函数编号是______．（写出所有真
命题的序号）