已知椭圆C的中心在原点,焦点在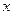 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的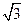 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为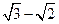 .
.
(1)求椭圆C的标准方程;
(2)若直线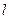 :
: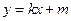 与圆O:
与圆O: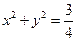 相切,且交椭圆C于A、B两点,
相切,且交椭圆C于A、B两点, 求当△AOB的面积最大时直线
求当△AOB的面积最大时直线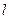 的方程.
的方程.
(本小题满分10分)已知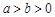 ,
,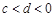 ,求证:
,求证: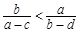 .
.
(本小题满分10分)在极坐标中,已知点 为方程
为方程 所表示的曲线上一动点,点
所表示的曲线上一动点,点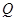 的坐标为
的坐标为 ,求
,求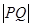 的最小值.
的最小值.
(本小题满分10分)已知矩阵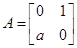 ,矩阵
,矩阵 ,直线
,直线 经矩阵
经矩阵 所对应的变换得到直线
所对应的变换得到直线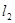 ,直线
,直线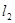 又经矩阵
又经矩阵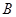 所对应的变换得到直线
所对应的变换得到直线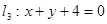 .
.
(1)求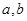 的值;
的值;
(2)求直线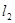 的方程.
的方程.
(本小题满分10分)如图所示,已知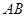 为圆
为圆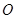 的直径,
的直径,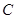 ,
,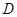 是圆
是圆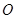 上的两个点,
上的两个点,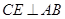 于
于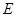 ,
,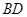 交
交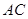 于
于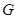 ,交
,交 于
于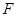 ,
,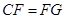 .
.
(1)求证: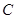 是劣弧
是劣弧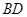 的中点;
的中点;
(2)求证: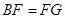 .
.
(本小题满分16分)已知函数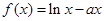 在
在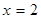 处的切线
处的切线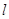 与直线
与直线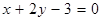 平行.
平行.
(1)求实数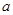 的值;
的值;
(2)若关于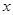 的方程
的方程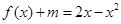 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数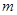 的取值范围;
的取值范围;
(3)记函数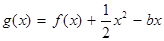 ,设
,设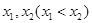 是函数
是函数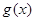 的两个极值点,若
的两个极值点,若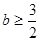 ,且
,且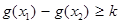 恒成立,求实数
恒成立,求实数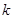 的最大值.
的最大值.