(本小题满分10分)
如图,设A是单位圆和x轴正半轴的交点,P,Q是单
位圆上的两点,D是坐标原点,∠AOP=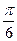 .∠AOQ=α,α∈[0,π).(Ⅰ)若Q(
.∠AOQ=α,α∈[0,π).(Ⅰ)若Q(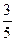 ,
,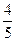 ),求cos(α-
),求cos(α-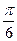 )的值; (Ⅱ)设函数f(α)=
)的值; (Ⅱ)设函数f(α)=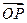 ·
·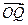 ,求f(α)的值域.
,求f(α)的值域.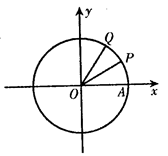
如图所示,四边形ABCD是矩形, ,F为CE上的点,且BF
,F为CE上的点,且BF 平面ACE,AC与BD交于点G
平面ACE,AC与BD交于点G
(1)求证:AE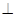 平面BCE
平面BCE
(2)求证:AE//平面BFD
已知函数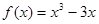
(1)求函数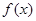 在
在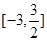 上的最大值和最小值.
上的最大值和最小值.
(2)过点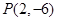 作曲线
作曲线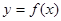 的切线,求此切线的方程.
的切线,求此切线的方程.
在直角坐标系 中,直线L的方程为x-y+4=0,曲线C的参数方程
中,直线L的方程为x-y+4=0,曲线C的参数方程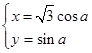
(1)求曲线C的普通方程;
(2)设点Q是曲线C上的一个动点,求它到直线L的距离的最小值.
已知直线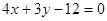 截圆心在点
截圆心在点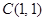 的圆
的圆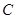 所得弦长为
所得弦长为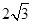 .
.
(1)求圆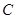 的方程;
的方程;
(2)求过点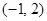 的圆
的圆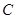 的切线方程.
的切线方程.
设函数f(x)=x3-3ax2+3bx的图像与直线12x+y-1=0相切于点(1,-11)。
(1)求a,b的值;
(2)讨论函数f(x)的单调性。