数列
的通项公式
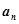=1-2n,其前n项和为
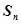，则数列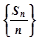
的前11项和为（ ）
| A．-45 | B．-50 | C．-55 | D．-66 |
设
是定义在R上的奇函数且单调递增，当
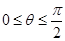时，
恒成立，则实数
的取值范围是（）
A． |
B． |
C． |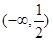
D． |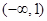
根据给出的数塔猜测123 456×9＋7＝ ( )
1×9＋2＝11
12×9＋3＝111
123×9＋4＝1 111
1 234×9＋5＝11 111
12 345×9＋6＝111 111
……
| A．1 111 110 | B．1 111 111 |
| C．1 111 112 | D．1 111 113 |
设
，
，
，……，
，
，则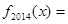
( )
A． |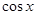
B． |
C． |
D． |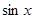
下列函数中，既是偶函数又在
上单调递增的是( )
A． |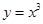
B． |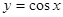
C． |
D． |
若“0<x<1”是“(x－a)[x－(a＋2)]≤0”的充分不必要条件，则实数a的取值范围是( )
| A．(－∞，0]∪[1，＋∞) | B．(－1,0) |
| C．[－1,0] | D．(－∞，－1)∪(0，＋∞) |