设a为实数，函数f(x)＝x3＋ax2＋(a－2)x的导数是f′(x)，且f′(x)是偶函数，则曲线y＝f(x)在原点处的切线方程为( )
| A．y＝－2x | B．y＝3x |
| C．y＝－3x | D．y＝4x |
已知e为自然对数的底数，则函数y＝xex的单调递增区间是( )
| A．[－1，＋∞) | B．(－∞，－1] |
| C．[1，＋∞) | D．(－∞，1] |
函数f(x)＝3x2＋ln x－2x的极值点的个数是( )
| A．0 | B．1 |
| C．2 | D．无数个 |
已知点A(a，b)与点B(1,0)在直线3x－4y＋10＝0的两侧，给出下列说法：
①3a－4b＋10>0；
②当a>0时，a＋b有最小值，无最大值；
③
>2；
④当a>0且a≠1，b>0时，
的取值范围为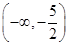
∪
.
其中正确的个数是( )
| A．1 | B．2 |
| C．3 | D．4 |
不等式x2＋2x<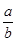
＋
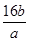对任意a，b∈(0，＋∞)恒成立，则实数x的取值范围是( )
| A．(－2,0) | B．(－∞，－2)∪(0，＋∞) |
| C．(－4,2) | D．(－∞，－4)∪(2，＋∞) |
在区间（0,4）上是减函数，则k的取值范围（ ）
