摆线是数学中众多迷人曲线之一,它是这样定义的:一个圆沿一直线无滑动地滚动,则圆上一固定点所经过的轨迹称为摆线.在竖直平面内有xOy坐标系,空间存在垂直xOy平面向里的匀强磁场,磁感应强度为B,一质量为m,电荷量为+q的小球从坐标原点由静止释放,小球的轨迹就是摆线.小球在O点速度为0时,可以分解为一水平向右的速度v0和一水平向左的速度v0两个分速度,如果v0取适当的值,就可以把摆线分解成以v0的速度向右做匀速直线运动和从O点向左速度为v0的匀速圆周运动两个分运动.设重力加速度为g,下列式子正确的是 ( )
| A.速度v0所取的适当值应为 |
| B.经过t=第一次到达摆线最低点 |
| C.最低点的y轴坐标为y=- |
| D.最低点的y轴坐标为y=- |
如图所示,直线OAC为某一直流电源的总功率随着电流变化的图线,抛物线OBC为同一直流电源内部的热功率随电流I变化的图线。若A、B对应的横坐标为2A,则下面说法中正确的是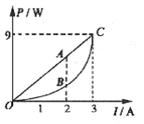
A.电源的电动势为3V,内阻为1Ω
B. 线段AB表示的功率为2W
C.电流为2A时,外电路电阻为0.5Ω
D. 电流为3A时,外电路电阻为2Ω
如图所示,竖直放置的螺线管与导线abcd构成回路,导线所围区域内有一垂直纸面向里的匀强磁场,螺线管下方水平桌面上有一导体圆环,导线abcd所围区域内磁场的磁感应强度按下图中哪一种图线随时间变化时,导体圆环将受到向上的磁场力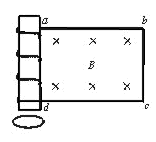
A. B. C. D.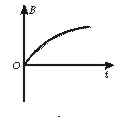
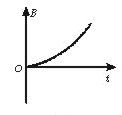
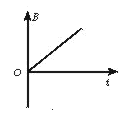 D.
D.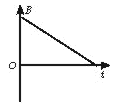
如图所示,是从一辆在水平公路上行驶着的汽车后方拍摄的汽车后轮照片。从照片来看,汽车此时正在( ) 
| A.直线前进 |
| B.向右转弯 |
| C.向左转弯 |
| D.不能判断 |
)下列说法正确的是
| A.普朗克曾经大胆假设:振动着的带电微粒的能量只能是某一最小能量值ε的整数倍,这个不可再分的最小能量值ε叫做能量子 |
B.德布罗意提出:实物粒子也具有波动性,而且粒子的能量ε和动量p跟它对所应的波的频率γ和波长λ之间,遵从关系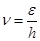 和 和 |
| C.光的干涉现象中,干涉亮条纹部分是光子到达几率大的地方 |
| D.在康普顿效应中,当入射光子与晶体中的电子碰撞时,把一部分动量转移给电子,因此,光子散射后波长变短 |
E.将放射性元素掺杂到其它稳定元素中,并降低其温度,它的半衰期将发生变化
下列说法中正确的是
| A.熵是物体内分子运动无序程度的量度 |
| B.若容器中用活塞封闭着刚好饱和的一些水汽,当保持温度不变向下缓慢压活塞时,水汽的质量减少,压强不变 |
| C.多晶体具有规则的几何外形,物理性质具有各向异性 |
| D.农民在干旱天气里锄松土壤是为了破坏土壤中的毛细管 |
E.用油膜法测出油分子的直径后,要测定阿伏加德罗常数,只需再知道油的密度即可