电磁炮是一种理想的兵器,它的主要原理如图所示。1982年澳大利亚制成了能把m= 2.0kg的弹体(包括金属杆EF的质量)加速到10km/s的电磁炮(常规炮弹的速度约为2km/s)。若轨道宽为2m,通过的电流为10A,轨道间所加匀强磁场的磁感强度为B=5×1O4T,B垂直于轨道向上 (轨道摩擦不计)求: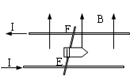
(1)弹体(包括金属杆EF)所受安培力大小;
(2)弹体(包括金属杆EF)从静止加速到10km/s,轨道至少要多长;
(3)弹体(包括金属杆EF)从静止加速到10km/s过程中,安培力
的最大瞬时功率。
A、B两车在同一直线上向右匀速运动,B车在A车前,A车的速度大小为V1=8m/s, B车的速度大小为V2=20m/s,如图所示。当A、B两车相距x0=28m时,B车因前方突发情况紧急刹车(已知刹车过程的运动可视为匀减速直线运动),加速度大小为a=2m/s2,从此时开始计时,求:
(1)A车追上B车之前,两者相距的最大距离;
(2)A车追上B车所用的时间;
(3)从安全行驶的角度考虑,为避免两车相撞,在题设条件下,求A车在B车刹车的同时也应刹车的最小加速度.
如图所示,在水平面上有两个用轻质弹簧相连接的物块A、B,它们的质量分别为m A 和m B ,弹簧的劲度系数为k,系统处于静止状态。现开始用一个恒力F沿竖直方向拉物块A使之向上运动,求: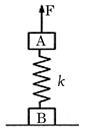
(1)系统处于静止状态时弹簧的压缩量;
(2)物块B刚要离开地面时弹簧的伸长量;
(3)从开始到物块B刚要离开地面时,物块A的位移d .
如下图所示,一个人用与水平方向成θ=37°角的斜向下的推力F推一个重G=200N的箱子匀速前进,箱子与地面间的动摩擦因数为μ=0.5(sin370=0.6,cos370=0.8,g=10m/s2)。
(1)求推力F的大小;
(2)若此人不改变推力F的大小,只把力的方向变为水平去推这个静止的箱子,则箱子做匀加速直线运动,推力作用时间t1=4s后撤去,撤去后箱子做匀减速直线运动,加速度大小均为a=5m/s2,求箱子滑行的总位移为多大?
一摩托车由静止开始在平直的公路上行驶,其运动过程的v-t图像如图所示,求: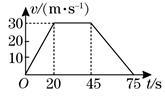
(1)摩托车在0-20s这段时间的加速度大小a;
(2)摩托车在0-75s这段时间的平均速度大小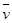 。
。
如图甲所示,水平面上的两光滑金属导轨平行固定放置,间距d=0.5 m,电阻不计,左端通过导线与阻值R=2 Ω的电阻连接,右端通过导线与阻值RL=4 Ω的小灯泡L连接。在CDFE矩形区域内有竖直向上的匀强磁场,CE长l=2 m,有一阻值r=2 Ω的金属棒PQ放置在靠近磁场边界CD处(恰好不在磁场中)。CDFE区域内磁场的磁感应强度B随时间变化如图乙所示。在t=0至t=4 s 内,金属棒PQ保持静止,在t=4 s时使金属棒PQ以某一速度进入磁场区域并保持匀速运动。已知从t=0开始到金属棒运动到磁场边界EF处的整个过程中,小灯泡的亮度没有发生变化。求: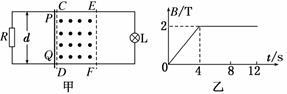
(1)通过小灯泡的电流;
(2)金属棒PQ在磁场区域中运动的速度大小。