如图所示，由物体A和B组成的系统处于静止状态．A、B的质量分别为mA和mB，且mA>mB．滑轮的质量和一切摩擦可不计。使悬绳的悬点由P点向右移动一小段距离到Q点，系统再次达到静止状态。当移动悬点后系统再次平衡时，B物体的位置( )
A．升高 B．降低
C．不变 D．不能确定
如图，足够长的U型光滑金属导轨平面与水平面成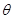
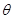角（0＜＜90°),其中MN与
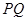平行且间距为L，导轨平面与磁感应强度为B的匀强磁场垂直，导轨电阻不计。金属棒
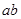由静止开始沿导轨下滑，并与两导轨始终保持垂直且良好接触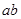，棒接入电路的电阻为R，当流过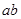棒某一横截面的电量为q时，棒的速度大小为
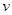，则金属棒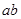在这一过程中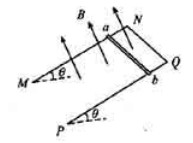
A．运动的平均速度大小为 |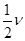
B．下滑的位移大小为 |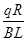
C．产生的焦耳热为 |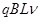
D．受到的最大安培力大小为 |
将闭合多匝线圈置于仅随时间变化的磁场中，线圈平面与磁场方向垂直，关于线圈中产生的感应电动势和感应电流，下列表述正确的是
| A．感应电动势的大小与线圈的匝数无关 |
| B．穿过线圈的磁通量越大，感应电动势越大 |
| C．穿过线圈的磁通量变化越快，感应电动势越大 |
| D．感应电流产生的磁场方向与原磁场方向始终相同 |
如图所示，在匀强磁场中匀速转动的矩形线圈的周期为T,转轴O1O2垂直于磁场方向，线圈电阻为2
.从线圈平面与磁场方向平行时开始计时，线圈转过60°时的感应电流为1A.那么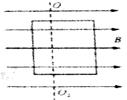
A.线圈消耗的电功率为4W
B.线圈中感应电流的有效值为2A
C.任意时刻线圈中的感应电动势为e = 4cos
D.任意时刻穿过线圈的磁通量为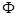
=
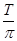sin
某同学为了验证断电自感现象，自己找来带铁心的线圈L、小灯泡A 、开关S和电池组E，用导线将它们连接成如图所示的电路。检查电路后，闭合开关s，小灯泡发光；再断开开关S，小灯泡仅有不显著的延时熄灭现象。虽经多次重复，仍未见老师演示时出现的小灯泡闪亮现象，他冥思苦想找不出原因。你认为最有可能造成小灯泡未闪亮的原因是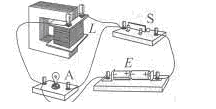 
A．电源的内阻较大
B．小灯泡电阻偏大
C．线圈电阻偏大
D．线圈的自感系数较大
在如图所示的电路中，两个相同的小灯泡L1和L2分别串联一个带铁芯的电感线圈L和一个滑动变阻器R.闭合开关S后，调整R，使L1和L2发光的亮度一样，此时流过两个灯泡的电流为I.然后，断开S.若t′时刻再闭合S，则在t′前后的一小段时间内，正确反映流过L1的电流i1、流过L2的电流i2随时间t变化的图象是( )