如图所示,固定于水平桌面上的金属框架cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动。此时abed构成一个边长为l的正方形,棒ab的电阻为r,其余部分电阻不计,开始时磁感应强度为B0。
⑴若 从t=0时刻起,磁感应强度均匀增加,每秒增加量为k,同时保持棒静止,求棒中的感应电流,并在图上标出电流方向;
从t=0时刻起,磁感应强度均匀增加,每秒增加量为k,同时保持棒静止,求棒中的感应电流,并在图上标出电流方向;
⑵在上述⑴情况下,始终保持棒静止,当t=t1时需施加垂直于棒的水平拉力多大?
⑶若从t=0时刻起,磁感应强度逐渐减小,当棒以恒定的速度v向右匀速运动时,可使棒中不产生感应电流,则磁感应强度怎样随时间变化( 写出B与t的关系式)?
写出B与t的关系式)?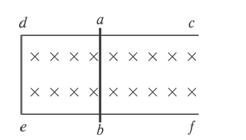
如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,磁感应强度B=0.50T的匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.50Ω的电阻,导轨宽度L=0.40m。金属棒ab紧贴在导轨上,现使金属棒ab由静止开始下滑,通过传感器记录金属棒ab下滑的距离h与时间t的关系如下表所示。(金属棒ab和导轨电阻不计,g=10m/s2)
| 时间t/s |
0 |
0.20 |
0.40 |
0.60 |
0.80 |
1.00 |
1.20 |
1.40 |
1 .60 .60 |
1.80 |
| 下滑距离h/m |
0 |
0.18 |
0.60 |
1.20 |
1.95 |
2.80 |
3.80 |
 4.80 4.80 |
5.80 |
6.80 |
求:(1)在前0. 4s的时间内,金属棒ab中的平均电动势;
4s的时间内,金属棒ab中的平均电动势;
(2)金属棒的质量m;
(3)在前1.60s的时间内,电阻R上产生的热量QR。
小球在外力作用下,由静止开始从A点出发做匀加速直线运动,到B点时消除外力。然后,小球冲上竖直平面内半径为R的光滑半圆环,恰能维持在圆环上做圆周运动,到达最高点C后抛出,最后落回到原来的出发点A处,如图所示,试求小球在AB段运动的加速度为多大?
太阳正处于主序星演化阶段,为了研究太阳演化进程,需知道 目前太阳的质量M。已知地球半径R= 6.4×106m,地球质量m =6.0
目前太阳的质量M。已知地球半径R= 6.4×106m,地球质量m =6.0 ×1024㎏,日地中心的距离r=1.5×1011 m,地球表面处的重力加速度g="10" m/s2,1年约为3.2×107 s,试估算目前太阳的质量M。
×1024㎏,日地中心的距离r=1.5×1011 m,地球表面处的重力加速度g="10" m/s2,1年约为3.2×107 s,试估算目前太阳的质量M。
如图,一质量为m=10kg的物体,由1/4光滑圆弧轨道上端从静止开始下滑,到达底端后沿水平面向右滑动1m距离后停止。已知轨道半径R=0.8m,g=10m/s2,求:
(1)物体滑至圆弧底端时的速度大小
(2)物体滑至圆弧底端时对轨道的压力大小
(3)物体沿水平面滑动过程中 克服摩擦力做的功
克服摩擦力做的功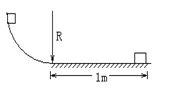
在距离地 面5米处将一个质量为1千克的小球以10m/s的速度水平抛出, 若g取10m/s2,问
面5米处将一个质量为1千克的小球以10m/s的速度水平抛出, 若g取10m/s2,问
(1)小球在空中的飞行时间是多少?
(2)水平飞行的距离是多少米?
(3)求小球落地时的速度