已知线段AB,在AB的延长线上取一点C,使AC=2BC,在AB的反向延长线上取一点D,使DA=2AB,那么线段AC是线段DB的( )倍.
A.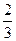 |
B.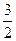 |
C.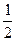 |
D.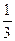 |
未来三年,国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿元用科学记数法表示为()
| A.0.845×104亿元 | B.8.45×103亿元 | C.8.45×104亿元 | D.84.5×102亿元 |
资阳市2012年财政收入取得重大突破,地方公共财政收入用四舍五入法取近似值后为27.39亿元.那么这个数值( )
| A.精确到亿位 | B.精确到百分位 | C.精确到千万位 | D.精确到百万位 |
在《关于促进城市南部地区加快发展第二阶段行动计划(2013-2015)》中,北京市提出了总计约3 960亿元的投资计划.将3 960用科学计数法表示应为()
| A.39.6×102 | B.3.96×103 | C.3.96×104 | D.3.96×104 |
用激光测距仪测得两物体之间的距离为14000000 米,将 14000000 用科学记数法表示为( )
A. |
B. |
C. |
D.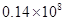 |
“辽宁号”航母是中国海军航空母舰的首舰,标准排水量57000吨,满载排水量67500吨.数据67500用科学记数法表示为()
| A.675×102 | B.67.5×103 | C.6.75×104 | D.6.75×105 |