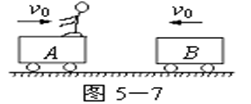
如图所示，在以O为圆心，半径为R＝10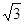
cm的圆形区域内，有一个水平方向的匀强磁场，磁感应强度大小为B＝0.1T，方向垂直纸面向外。竖直平行放置的两金属板A、K相距d＝20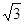mm，接在如图所示的电路中，电源电动势E＝91V，内阻r＝1Ω定值电阻R1＝10Ω，滑动变阻器R2的最大阻值为80Ω，S1、S2为A、N板上的两个小孔，且S1、S2跟O点在垂直极板的同一直线上，
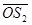＝2R。另有一水平放置的足够长的荧光屏D，O点跟荧光屏D之间的距离为H＝2R。比荷为2×105C/kg的正离子流由S1进入电场后，通过S2向磁场中心射去，通过磁场后落到荧光屏D上。离子进入电场的初速度、重力、离子之间的作用力均可忽略不计。求：当滑动片P处于最右端时，，正离子打在荧光屏上具的落点到圆心O的水平距离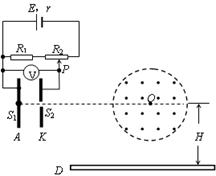
如图甲所示，一个电阻值为R、匝数为n的圆形金属线圈与阻值为2R的电阻R1连接成闭合回路．线圈的半径为r1，在线圈中半径为r2的圆形区域内存在垂直于线圈平面向里的匀强磁场，磁感应强度B随时间t变化的关系图线如图乙所示．图线与横、纵轴的截距分别为t0和B0，导线的电阻不计．求0至t1时间内：
(1)通过电阻R1上的电流大小和方向；
(2)通过电阻R1上的电荷量q及电阻R1上产生的热量．
如图所示，匀强磁场的磁感应强度B＝0.1 T，金属棒AD长0.4 m，与框架宽度相同，电阻r＝1/3 Ω，框架电阻不计，电阻R1＝2 Ω，R2＝1 Ω.当金属棒以5 m/s速度匀速向右运动时，求：
(1)流过金属棒的感应电流为多大？
(2)若图中电容器C为0.3 μF，则电容器中储存多少电荷量？
如图所示，固定于水平面上的金属架CDEF处在竖直向下的匀强磁场中，金属棒MN沿框架以速度v向右做匀速运动．t＝0时，磁感应强度为B0，此时MN到达的位置使MDEN构成一个边长为l的正方形．为使MN棒中不产生感应电流，从t＝0开始，磁感应强度B应怎样随时间t变化？请推导出这种情况下B与t的关系式．
一个电子和一个正电子对撞发生湮灭而转化为一对光子，设正负电子对撞前的质量均为m，动能均为Ek，光速为c，普朗克常量恒为h.求：
①写出该反应方程；
②对撞过程中的质量亏损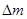
和转化成的光子在真空中波长λ．
如图所示，有A、B两质量为M= 100kg的小车，在光滑水平面以相同的速率v0=2m/s在同一直线上相对运动，A车上有一质量为m = 50kg的人至少要以多大的速度（对地）从A车跳到B车上，才能避免两车相撞？