(本题满分7分)
在日常生活中,我们经常有目的地收集数据,分析数据,作出预测,
(1)图7是小芳家2010年全年月用电量的条形统计图. .
根据图中提供的信息,回答下列问题:
①2010年小芳家月用电量最小的是_____月,四个季度中用电量最大的是第___季度;
②求2010年5月至6月用电量的月增长率;
(2)2011年小芳家准备添置新电器.假设2011年5月份的用电量是120千瓦时,根据2010年5月至7月用电量的增长趋势,预计2011年7月份的用电量将达到240千瓦时.假设2011年5月至6月用电量月增长率是6月至7月用电量月增长率的1.5倍,预计小芳家2011年6月份的用电量是多少千瓦时?
“铁路建设助推经济发展”,近年来我国政府十分重视铁路建设。渝利铁路通车后,从重庆到上海比原铁路全程缩短了320千米,列车设计运行时速比原铁路设计运行时速提高了l20千米/小时,全程设计运行时间只需8小时,比原铁路设计运行时间少用16小时.
(1)渝利铁路通车后,重庆到上海的列车设计运行里程是多少千米?
(2)专家建议:从安全的角度考虑,实际运行时速要比设计时速减少m%,以便于有充分时间应对突发事件,这样,从重庆到上海的实际运行时间将增加 m小时,求m的值.
m小时,求m的值.
为了弘扬九十五中学办学理念,我校将“立己立人,尽善尽美”的校训印在旗帜上,放置在教学楼的顶部(如图所示)。小华在教学楼前空地上的点D处,用1米高的测角仪CD,从点C测得旗帜的底部B的仰角为37°,然后向教学楼正方向走了4.8米到达点F处,又从点E测得旗帜的顶部A的仰角为45°。若教学楼高BM=19米,且点A、B、M在同一直线上,求旗帜AB的高度(参考数据:sin37°≈0.60,cos37°≈0.81,tan37°≈0.75)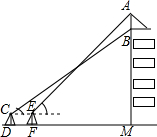
先化简,再求值: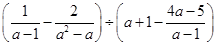
重庆市“创建文明城市”活动如火如荼的展开,我校为了搞好“创建文明城市”活动的宣传。校学生会就本校学生对重庆市“市情市况”的了解程度进行了一次调查测试。经过对测试成绩的分析,得到如下图所示的不完整的统计图(A:59分及以下;B:60-69分;C:70-79分;D:80-89分;E:90-100分)。请你根据图中提供的信息解答以下问题: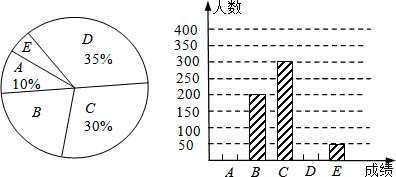
(1)请将条形统计图补充完整;
(2)其中男生小明、小刚和女生小红、小兰测试成绩为E,学校决定从这4名同学中选两名代表参加市级比赛,请你用画树状图或列表格的方法求出所选两名同学恰为一男一女的概率。
如图,已知点E、C在线段BF上,BE=CF,AB∥DE,AB=DE,求证:AC∥DF