如图12所示，长L=1.6m，质量M=3kg的木板静放在
光滑水平面上，质量m=1kg、
带电量q=+2.5×10-4C的小滑块放在木板的右端，木板和物块间的动摩擦因数μ=0.1，所在空间加有一个方向竖直向下强度为E=4.0×104N/C的匀强电场，如图所示，现对木板施加一水平向右的拉力F．取g=10m/s2，求：
（1）使物块不掉下去的最大拉力F；
（2）如果拉力F=11N恒定不变，小物块所能获得的最大动能.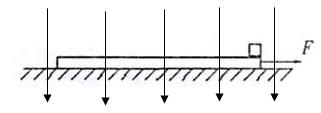
如图甲所示，一半径R＝1m、圆心角等于143°的竖直圆弧形光滑轨道，与斜面相切于B处，圆弧轨道的最高点为M，斜面倾角θ＝37°，t＝0时刻有一物块从斜面底端A处沿斜面上滑，其在斜面上运动的速度变化规律如图乙所示．若物块恰能到达M点，（取g＝10m/s2，sin37°＝0.6，cos37°＝0.8），求：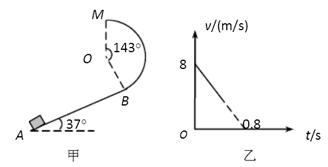
（1）物块经过B点时的速度；
（2）物块与斜面间的动摩擦因数μ.
隧道是高速公路上的特殊路段也是事故多发路段之一。某日，一货车A因故障恰停在隧道内离隧道入口d="50" m的位置。此时另一轿车B正以v0="25" m/s的速度匀速向隧道口驶来，轿车B的驾驶员在进入隧道口时，才发现停在前方的货车A并立即采取制动措施。假设该驾驶员反应时间t="0.6" s，轿车制动时受到的阻力恒为自身重力的0.75倍，取g="10" m/s2。
（1）试通过计算说明轿车B是否会与停在前面的货车A相撞?
（2）若会相撞，那么撞前瞬间轿车B速度大小为多少?若不会相撞，那么停止时与货车A的距离为多少？
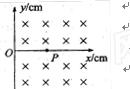
如图所示，在第二象限内有水平向右的匀强电场，在第一、第四象限内分别存在匀强磁场，磁感应强度大小相等，方向如图所示．现有一个带电粒子在该平面内从X轴上的P点，以垂直于X轴的初速度
进入匀强电场，恰好经过y轴上的Q点且与y轴成450角射出电场，再经过一段时间又恰好垂直于X轴进入下面的磁场．已知OP之间的距离为d（不计粒子的重力）求：
（1）Q点的坐标；
（2）带电粒子自进入电场至在磁场中第二次经过X轴的时间．
如图所示，在匀强磁场中倾斜放置两根平行金属导轨，导轨与水平面夹角为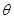
，磁场方向垂直导轨平面向下，磁感应强度的大小为B，平行导轨间距为L。两根金属杆ab和cd可以在导轨上无摩擦地滑动。两金属杆的质量均为m，电阻均为R，导轨的电阻不计。若用与导轨平面平行的拉力F作用在金属杆ab上，使ab匀速上滑，cd杆在导轨上恰好保持静止。求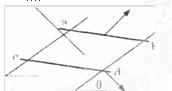
（1）拉力F的大小，
（2）ab杆上滑的速度大小。
如图所示，在真空中坐标xOy平面的x>0区域内，有磁感应强度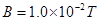
的匀强磁场，方向与xoy平面垂直，在x轴上的P（10，0）点，有一放射源，在xoy平面内向各个方向发射速率
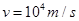的带正电的粒子，粒子的质量为
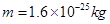，电荷量为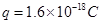
，求带电粒子能打到y轴上的范围．