如图，点P的坐标为（2，
），过点P作x轴的平行线交y轴于点A，交双曲线
(x>0)于点N；作PM⊥AN交双曲线(x>0)于点M，连结AM.已知PN=4.
（1）求点N坐标及k的值.
（2）求M点坐标及△AMN的面积.
如图，点E，F在BC上，BE＝CF，AB＝DC，∠B＝∠C.
求证：∠A＝∠D.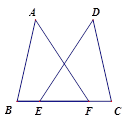
解方程：
如图，在平面直角坐标系xOy中，抛物线
过点
，这条抛物线的对称轴与x轴交于点C，点P为射线CB上一个动点（不与点C重合），点D为此抛物线对称轴上一点，且CPD=
．
（1）求抛物线的解析式；
（2）若点P的横坐标为m，△PCD的面积为S，求S与m之间的函数关系式；
（3）过点P作PE⊥DP，连接DE，F为DE的中点，试求线段BF的最小值．
在△ABC中，AB=AC，∠A=300，将线段BC绕点B逆时针旋转600得到线段BD，再将线段BD平移到EF，使点E在AB上，点F在AC上．
（1）如图1，直接写出∠ABD和∠CFE的度数；
（2）在图1中证明：AE=CF；
（3）如图2，连接CE，判断△CEF的形状并加以证明．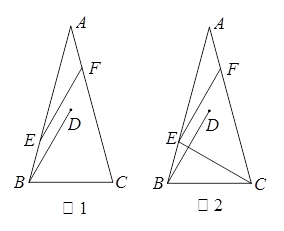
已知关于
的一元二次方程
．
（1）求证：方程总有两个实数根；
（2）若m为整数，当此方程有两个互不相等的负整数根时，求m的值；
（3）在（2）的条件下，设抛物线
与x轴交点为A、B（点B在点A的右侧），与y轴交于点C．点O为坐标原点，点P在直线BC上，且OP=
BC，求点P的坐标．