如图所示,在水平向左足够大的匀强电场中,一带电小球用绝缘轻绳悬于O点,平衡时小球位于A点, 此时绳与竖直方向的夹角 =53°,已知绳长
=53°,已知绳长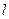 ,B、C、D到O点的距离均为
,B、C、D到O点的距离均为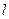 ,BD水平,OC竖直.
,BD水平,OC竖直.
(1)将小球移到B点,给小球一竖直向下的初速度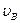 ,小球到达悬点正下方时绳中拉力恰等于小球重力,求
,小球到达悬点正下方时绳中拉力恰等于小球重力,求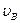 .
.
(2)将小球移到D点,给小球一斜向右上方的初速度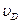 ,初速度
,初速度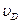 的方向与水平方向的夹角为53°,小球恰好能经过B点. 求小球在D点时初速度
的方向与水平方向的夹角为53°,小球恰好能经过B点. 求小球在D点时初速度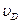 的大小.(取
的大小.(取 ,
,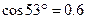 )
)
一个物体从45m高处自由下落,取g=10m/s2,则:
(1)经过多长时间落到地面?
(2)落到地面的瞬间物体的速度是多少?
滑板运动是一项非常刺激的水上运动(如图所示),研究表明,在进行滑板运动时,水对滑板的作用力N垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力F作用下,当滑板和水面的夹角θ=37°时,滑板做匀速直线运动,相应的k=40kg/m,人和滑板的总质量为80kg,(重力加速度g取10m/s2,sin 37°=0.6,忽略空气阻力). 试求:
(1)水平牵引力F的大小;
(2)滑板的速率v=?
【考点】共点力平衡的条件及其应用;力的合成与分解的运用.菁优网版权所有
【专题】共点力作用下物体平衡专题.
【分析】(1)对滑板和人整体受力分析,然后运用共点力平衡条件列式求解;
(2)根据平衡条件求出支持力后,根据题中的支持力和速度关系公式求解滑板的速率.
如图所示,质量为m,横截面积为直角三角形的物块ABC,∠ABC=α,AB边靠在竖直墙面上,物块与墙面间的动摩擦因数为μ,现物块在垂直于斜面BC的推力作用下,沿墙面匀速滑行.试表示出力F的大小.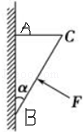
如图所示,用绳AC和BC吊起一重物,绳与竖直方向夹角分别为30°和60°,AC绳能承受的最大拉力为150N,而BC绳能承受的最大拉力为100N,求物体最大重力不能超过多少?
小车从静止开始以1m/s2的加速度前进,车后相距x0=25m处,与车运动方向相同的某人同时开始以6m/s的速度匀速追车,问能否追上?若追不上,求人、车间的最小距离是多少?