如图所示,在粗糙绝缘水平面的A、B两处,分别固定着两个带相等电荷量的正点电荷,A、B相距4 L,O点是AB连线的中点,a、b是AB连线上的两点,且aO=bO=L。一质量为m,电荷量为q的带正电小滑块(可以看作质点)以初动能Eko从a点出发,沿直线向B点运动,小滑块第一次经过O点时动能为3Eko,第一次到达6点时动能恰好为零,小滑块最终停在O点。题中L、Eko、q和重力加速度g均为已知量,则下列说法正确的是 ( )
A.因两点电荷的电荷量、静电力常量题中均未知,故无法计算出小滑块运动的总路程
B.因两点电荷的电荷量、静电力常量题中均未知,故无法计算出电场中b、O两点的电势差
C.从题中数据可以确定小滑块与水平面间的动摩擦因数
D.小滑块第一次从a到O的过程中,电场力对它做的功等于小滑块增加的机械能
下列关于电源电动势的说法正确的是()
| A.电源是通过静电力把其它形式的能转化为电能的装置 |
| B.在电源内部正电荷从低电势处向高电势处移动 |
| C.电源电动势反映了电源内部静电力做功的本领 |
| D.把同一电源接在不同的电路中,电源的电动势也将变化 |
关于静电场,下列结论普遍成立的是()
| A.电场强度大的地方电势高,电场强度小的地方电势低 |
| B.电场中任意两点之间的电势差只与这两点的场强有关 |
| C.在正电荷或负电荷产生的静电场中,场强方向都指向电势降低最快的方向 |
| D.在电场强度越大的地方,电荷的电势能也越大 |
如图所示,在倾角为α的斜面上,放一质量为m的小球,小球和斜坡及挡板间均无摩擦,当档板绕O点逆时针缓慢地转向水平位置的过程中( )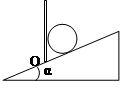
| A.斜面对球的支持力逐渐增大 |
| B.斜面对球的支持力逐渐减小 |
| C.档板对小球的弹力先减小后增大 |
| D.档板对小球的弹力先增大后减小 |
物体A、B都静止在同一水平面上,它们的质量分别为MA、MB,与水平面间的动摩擦因数分别为μA、μB,平行于水平面的拉力F分别拉物体A、B,测得加速度a与拉力F的关系图象如图中A、B所示,则( )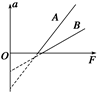
A.μA>μB B.μA<μB C.MA>MB D.MA<MB
建筑工人用如图所示的定滑轮装置运送建筑材料.质量为70.0 kg的建筑工人站在地面上,通过定滑轮将20.0 kg的建筑材料以0.5 m/s2的加速度竖直加速拉升,忽略绳子和定滑轮的质量及定滑轮的摩擦,则建筑工人对绳子的拉力F1及对地面的压力F2大小分别为(g取10 m/s2) ( )
| A.F1=200N | B.F1=210N | C.F2="490" N | D.F2=700N |