如图所示，一质量为M=2kg的绝缘滑板静止于水平面上，它与水平面闻的动摩擦因数为
=0.1，绝缘滑板上表面0点的左侧是光滑的，O点的右侧是粗糙的。有质量均为m="1" kg的小物块a、b分别静止地放于绝缘滑板的A点和O点，且A点与O点的间距L="0.5" m，小物块a、b均可视为质点，它们在O点右侧时与绝缘滑板间动摩擦因数均为弘- -
整个装置所在空间存在着E=8×l03 N/C且方向水平向右的匀强电场，小物块a带有q=5×10-4C的正电荷，b和滑板均不带电。若小物块在运动过程中电荷量始终不变，a与b相碰后粘合在一起且碰撞时间极短，小物块恰好能到达绝缘滑板的右端；最大静摩擦力在大小上等于滑动摩擦力，g取10m／s2。求：
（1）小物块a到达O点时的速度。
（2）绝缘滑板的长度。
一段凹槽B放置在水平面上，槽与水平面间的动摩擦因数μ=0.5，槽的内表面光滑，在内表面上有一小球A靠左侧壁放置，此时小球A与槽的右侧壁相距为l，如图所示．A、B的质量均为m．现对槽B施加一个大小等于2mg（g为重力加速度）、方向水平向右的推力F，使B和A一起从静止开始向右运动，当槽B运动的距离为d时，立刻将推力撤去，此后A和B发生相对运动，再经一段时间球A碰到槽的右侧壁． 
（1）求撤去推力瞬间槽B的速度v的大小．
（2）试讨论球A相对于槽从左侧壁运动至右侧壁所经过的时间t与l和d的关系．
如图，圆形玻璃平板半径为R，离水平地面的高度为h，可绕圆心O在水平面内自由转动，一质量为m的小木块放置在玻璃板的边缘．玻璃板匀速转动使木块随之做匀速圆周运动．
（1）若已知玻璃板匀速转动的周期为T，求木块所受摩擦力的大小．
（2）缓慢增大转速，木块随玻璃板缓慢加速，直到从玻璃板滑出．已知木块脱离时沿玻璃板边缘的切线方向水平飞出，落地点与通过圆心O的竖直线间的距离为s．木块抛出的初速度可认为等于木块做匀速圆周运动即将滑离玻璃板时的线速度，滑动摩擦力可认为等于最大静摩擦力，试求木块与玻璃板间的动摩擦因数μ．
如图10所示，质量为m的小球，由长为l的细线系住，线能承受的最大拉力是9mg，细线的另一端固定在A点，AB是过A的竖直线，E为AB上的一点，且AE=0.5l，过E作水平线EF，在EF上钉铁钉D，现将小球拉直水平，然后由静止释放，小球在运动过程中，不计细线与钉子碰撞时的能量损失，不考虑小球与细线间的碰撞．
（1）若钉铁钉位置在E点，求细线与钉子碰撞前后瞬间，细线的拉力分别是多少？
（2）若小球能绕钉子在竖直面内做完整的圆周运动，求钉子位置在水平线EF上距E点距离的取值。
如图，细绳一端系着质量M=0.6kg的物体，静止在水平面，另一端通过光滑小孔吊着质量m=0.3kg的物体，M的中点与圆孔距离为0.2m，并知M和水平面的最大静摩擦力因数为μ=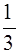
，现使此平面绕中心轴线转动，问角速度w在什么范围m会处于静止状态？(g取10m/s2)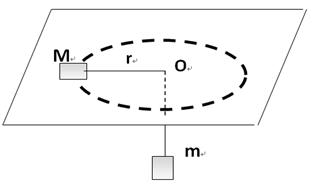
放在水平地面上一质量为m＝2kg的质点，在水平恒定外力作用下由静止开始沿直线运动，4 s内通过8 m的距离，此后撤去外力，质点又运动了2 s停止，质点运动过程中所受阻力大小不变，求：
(1)撤去水平恒定外力时质点的速度大小；
(2)质点运动过程中所受到的阻力大小；
(3)质点所受水平恒定外力的大小．