椭圆E经过点A(2,3),对称轴为坐标轴,焦点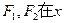 轴上,离心率
轴上,离心率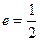
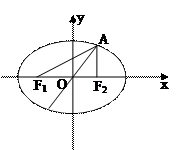
(I)求椭圆E的方程;
(II)求 的角平分线所在直线的方程
的角平分线所在直线的方程
已知偶函数f(x)在(0,+∞)上为增函数,且f(2)=0,解不等式f[log2(x2+5x+4)]≥0.
已知奇函数f(x)的定义域为R,且f(x)在[0,+∞)上是增函数,是否存在实数m,使f(cos2θ-3)+f(4m-2mcosθ)>f(0)对所有θ∈[0, ]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
]都成立?若存在,求出符合条件的所有实数m的范围,若不存在,说明理由。
已知奇函数f(x)是定义在(-3,3)上的减函数,且满足不等式f(x-3)+f(x2-3)<0,设不等式解集为A,B=A∪{x|1≤x≤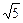 },求函数g(x)=-3x2+3x-4(x∈B)的最大值。
},求函数g(x)=-3x2+3x-4(x∈B)的最大值。
设m是实数,记M={m|m>1},f(x)=log3(x2-4mx+4m2+m+ )
)
(1)证明: 当m∈M时,f(x)对所有实数都有意义;反之,若f(x)对所有实数x都有意义,则m∈M。
(2)当m∈M时,求函数f(x)的最小值。
(3)求证: 对每个m∈M,函数f(x)的最小值都不小于1。
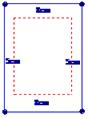
设计一幅宣传画,要求画面面积为4840 cm2,画面的宽与高的比为λ(λ<1),画面的上、下各留8 cm的空白,左右各留5 cm空白,怎样确定画面的高与宽尺寸,才能使宣传画所用纸张面积最小?
如果要求λ∈[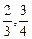 ],那么λ为何值时,能使宣传画所用纸张面积最小?
],那么λ为何值时,能使宣传画所用纸张面积最小?