如图甲,在平面四边形ABCD中,已知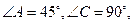
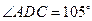 ,
, ,现将四边形ABCD沿BD折起,
,现将四边形ABCD沿BD折起,
使平面ABD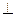 平面BDC(如图乙),设点E、F分别为棱
平面BDC(如图乙),设点E、F分别为棱
AC、AD的中点.
(1)求证:DC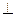 平面ABC;
平面ABC;
(2)求BF与平面ABC所成角的正弦;
(3)求二面角B-EF-A的余弦.


|
|||
|
|||
抛掷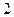 颗质地均匀的骰子,求点数和为
颗质地均匀的骰子,求点数和为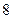 的概率。
的概率。
袋中有大小相同的红、黄两种颜色的球各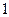 个,从中任取
个,从中任取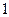 只,有放回地抽取
只,有放回地抽取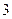 次.求:
次.求:
①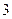 只全是红球的概率;
只全是红球的概率;
②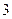 只颜色全相同的概率;
只颜色全相同的概率;
③ 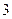 只颜色不全相同的概率.
只颜色不全相同的概率.
一个路口的红绿灯,红灯的时间为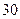 秒,黄灯的时间为
秒,黄灯的时间为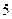 秒,绿灯的时间为
秒,绿灯的时间为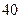 秒,当你到达路口时看见下列三种情况的概率各是多少?
秒,当你到达路口时看见下列三种情况的概率各是多少?
(1) 红灯 (2) 黄灯 (3)不是红灯
某路公共汽车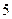 分钟一班准时到达某车站,求任一人在该车站等车时间少于
分钟一班准时到达某车站,求任一人在该车站等车时间少于 分钟的概率(假定车到来后每人都能上)
分钟的概率(假定车到来后每人都能上)
现有一批产品共有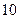 件,其中
件,其中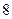 件为正品,
件为正品,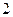 件为次品:
件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续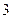 次取出的都是正品的概率;(2)如果从中一次取
次取出的都是正品的概率;(2)如果从中一次取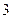 件,求
件,求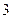 件都是正品的概率.
件都是正品的概率.