如图,在平面直角坐标系中,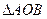 的顶点A(
的顶点A(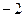 ,0)、B(
,0)、B(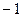 ,1)。将
,1)。将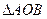 绕点O顺时针旋转
绕点O顺时针旋转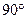 后,点A、B分别落在
后,点A、B分别落在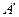 、
、  。
。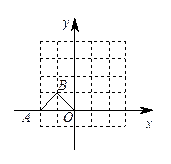
(1)在图中画出旋转后的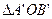 ;
;
(2)求点A旋转到点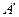 所经过的弧形路线长
所经过的弧形路线长
已知抛物线m: ,顶点为A,若将抛物线m绕着点(1,0)旋转180°后得到抛物线n,顶点为C.
,顶点为A,若将抛物线m绕着点(1,0)旋转180°后得到抛物线n,顶点为C.当a=1时.试求抛物线n的顶点C的坐标,再求它的解析式;
在(1)中,请你分别在抛物线m、n上各取一点D、B(除点A、C外),
使得四边形ABCD为平行四边形(直接写出所取点的坐标,并至少写出二种情况);设抛物线m的对称轴与抛物线n的交点为P,且
 =6,试求a的值.
=6,试求a的值.
某校为了解初中生的交通安全知识掌握情况,在本校初中部随机抽取10﹪的学生,进行了交通安全知识测试,得分情况如下两个统计图,并约定85分及以上为优秀;73分~84分为良好;60分~72分为合格;59分及以下为不合格(满分为100分).在抽取的学生中,不合格人数所占的百分比是;
若不合格学生的总分恰好等于其他等级的某一个学生的分数,请推测这个学生是什么等级?并估算出该校初中部学生中共有多少人不合格?
试求所抽取的学生的平均分.
 .
.
如图,同心⊙O,大⊙O的直径AB=2 ,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.
,小⊙O的直径CD=2,连接AC、AD、BD、BC,AD、CB分别交小⊙O于E、F.问四边形CEDF是何种特殊四边形?请证明你的结论;
当AC与小⊙O相切时,四边形CEDF是正方形吗?请说明理由.

在2012年元旦期间有甲、乙两个小型超市举行有奖促销活动,顾客每购货20元就有一回按下面规则转盘获奖机会,且两超市奖额等同.规则是甲、乙两超市各把一转盘分成4个、3个区域,并标上了数字(如图甲、乙),顾客一回转盘要转两次,第一次与第二次分别停止后指针所指数字之和为奇数时就获奖(若指针停在等分线上,那么重转一次,直到指针指向某一份为止).利用树形图或列表法分别求出甲、乙两超市顾客一回转盘获奖的概率;
如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.

如图1,是某单位的透空护栏,如图2是它的示意图,它是用外径为3cm的圆钢管与外圆直径为15cm的圆圈焊接而成的(圆圈由扁钢筋做成,两圆钢管之间夹一个圆圈),若要做高度统一为2m,长为7.41m的护栏.试问:需要圆钢管和展直扁钢筋的总长度各是多少m?