如图所示,一块质量为M的木板停在光滑的水平面上,木板的左端有挡板,挡板上固定一个小弹簧。一个质量为m的小物块(可视为质点)以水平速度υ0从木板的右端开始向左运动,与弹簧碰撞后(弹簧处于弹性限度内),最终又恰好停在木板的右端。根据上述情景和已知量,可以求出
| A.弹簧的劲度系数 |
| B.弹簧的最大弹性势能 |
| C.木板和小物块之间的动摩擦因数 |
| D.木板和小物块组成的系统最终损失的机械能 |
如图所示的电路中,当变阻器R3的滑动触头P向a端移动时()
| A.电压表示数变大,电流表示数变小 |
| B.电压表示数变小,电流表示数变大 |
| C.电压表示数变大,电流表示数变大 |
| D.电压表示数变小,电流表示数变小 |

图中电阻R1、R2、R3的阻值相等,电池的内阻不计。开关K接通后,流过R2的电流是K接通前的()
A. |
B.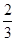 |
C. |
D. |
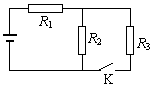
在“测定电源电动势和内阻”的实验中,针对两个不同的电源得出如右图所示的1、2两条图线,则两个电源的动势E1和E2、内阻r1和r2满足关系)
| A.E1>E2,r1>r2 | B.E1>E2,r1<r2 |
| C.E1<E2,r1<r2 | D.E1<E2,r1>r2 |
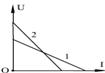
如图,平行板电容器的两个极板与水平地面成一角度,两极板与一直流电源相连。若一带电粒子恰能沿图中所示水平直线通过电容器,则在此过程中,该粒子( )
| A.所受重力与电场力平衡 |
| B.电势能逐渐增加 |
| C.动能逐渐增加 |
| D.做匀变速直线运动 |

如图所示,质量、电量分别为m1、m2、q1、q2的两球,用绝缘丝线悬于同一点,静止后它们恰好位于同一水平面上,细线与竖直方向夹角分别为α、β,则( )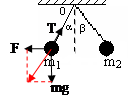
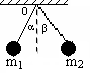
| A.若m1=m2,q1<q2,则α<β |
| B.若m1=m2,q1<q2,则α>β |
| C.若q1=q2,m1>m2,则α>β |
| D.q1、q2是否相等与α、β大小无关,且若m1>m2,则α<β |