对于函数①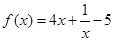 ,②
,②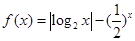 ,③
,③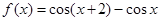 ,判断如下两个命题的真假:
,判断如下两个命题的真假:
命题甲: 在区间
在区间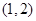 上是增函数;
上是增函数;
命题乙: 在区间
在区间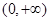 上恰有两个零点
上恰有两个零点 ,且
,且 .能使命题甲、乙均为真的函数的序号是
.能使命题甲、乙均为真的函数的序号是
| A.① | B.② | C.①③ | D.①② |
已知双曲线  的左、右焦点分别是
的左、右焦点分别是 、
、 过
过 垂直x轴的直线与双曲线C的两渐近线的交点分别是M、N,若
垂直x轴的直线与双曲线C的两渐近线的交点分别是M、N,若 为正三角形,则该双曲线的离心率为()
为正三角形,则该双曲线的离心率为()
A. |
B. |
C. |
D. |
已知函数  ,执行右边的程序框图,若输出的结果是
,执行右边的程序框图,若输出的结果是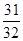 ,则
,则
判断框中的条件应是()
A. |
B. |
C.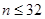 |
D.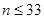 |
已知  表示平面,m,n表示直线,
表示平面,m,n表示直线, 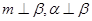 ,给出下列四个结论:
,给出下列四个结论:
①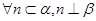 ;②
;②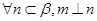 ;③
;③ ;④
;④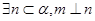 ,
,
则上述结论中正确的个数为()
| A.1 | B.2 | C.3 | D.4 |
已知 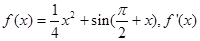 为
为  的导函数,则
的导函数,则  的图象大致是()
的图象大致是()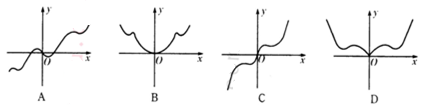
为了调查学生携带手机的情况,学校对高一、高二、高三三个年级的学生进行分层抽样调查,已知高一有学生l000人、高二有1200人;三个年级总共抽取了66人,其中高一抽取了20人,则高三年级的全部学生数为()
| A.1000 | B.1100 | C.1200 | D.1300 |