如图所示,有一个矩形线圈,质量m=0.016kg,长L=0.5m,宽d=0.1m,电阻R=0.1Ω。从离匀强磁场上边缘高h=5m处由静止自由下落,进入磁场时,线圈恰能做匀速运动。不计空气阻力,H>h,取g=l0m/s2。求:
(1)匀强磁场的磁感应强度大小.
(2)线圈由位置1到完全进入磁场的过程中,线框中产生的热量。
一自行车以6m/s的速度沿平直的公路匀速运动,一小汽车从静止开始与自行车同向做匀加速运动,加速度大小为3m/s2;汽车开始运动时,自行车恰好与汽车车头相齐.求:
(1)汽车追上自行车之前经多长时间两者相距最远?最远距离是多少?
(2)汽车经过多长时间追上自行车?此时汽车的速度是多少?
如图所示,OA、OB、OC三段轻绳结于O点,OB水平且与放置在水平面上质量为m1=1.5kg的物体乙相连,OC下方悬挂物体甲.此时物体乙恰好未滑动,已知OA与竖直方向的夹角θ=37°,物体乙与地面间的动摩擦因数μ=0.2,可以认为最大静摩擦力与滑动摩擦力相等.g=10m/s2(sin37°=0.6,cos37°=0.8)求: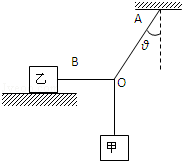
(1)OB绳对物体乙的拉力是多大?
(2)物体甲的质量m2为多少?
如图所示,与水平面夹角为30°的固定斜面上有一质量m=1.0kg的物体.细绳的一端通过摩擦不计的定滑轮与固定的弹簧秤相连.物体静止在斜面上,弹簧秤的示数为6N,(取g=10m/s2),求物体所受的支持力和摩擦力.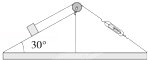
如图所示,一个重为100N的小球被夹在竖直的墙壁和A点之间,已知球心O与A点的连线与竖直方向成θ角,且θ=60°,所有接触点和面均不计摩擦.试求小球对墙面的压力F1和对A点压力F2.
如图所示为货场使用的传送带的模型,传送带倾斜放置,与水平面夹角为θ=37°,传送带AB长度足够长,传送皮带轮以大小为υ=2m/s的恒定速率顺时针转动.一包货物以υ0=12m/s的初速度从A端滑上倾斜传送带,若货物与皮带之间的动摩擦因数μ=0.5,且可将货物视为质点.
(1)求货物刚滑上传送带时加速度为多大?
(2)经过多长时间货物的速度和传送带的速度相同?这时货物相对于地面运动了多远?
(3)从货物滑上传送带开始计时,货物再次滑回A端共用了多少时间?(g=10m/s2,已知sin37°=0.6,cos37°=0.8)