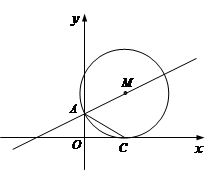已知抛物线y＝ax2＋bx＋c经过A（－4，3）、B（2，0）两点，当x=3和x=－3时，这条抛物线上对应点的纵坐标相等．经过点C（0，－2）的直线l与 x轴平行，O为坐标原点．
（1）求直线AB和这条抛物线的解析式；
（2）以A为圆心，AO为半径的圆记为⊙A，判断直线l与⊙A的位置关系，并说明理由；
（3）设直线AB上的点D的横坐标为－1，P（m，n）是抛物线y＝ax2＋bx＋c上的动点，当△PDO的周长最小时，求四边形CODP的面积．
先化简，再求值：
，其中a＝
．
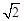解不等式组
，并写出该不等式组的最大整数解．
如图1，在等腰△ABC中，底边BC＝8，高AD＝2，一动点Q从B点出发，以每秒1个单位的速度沿BC向右运动，到达D点停止；另一动点P从距离B点1个单位的位置出发，以相同的速度沿BC向右运动，到达DC中点停止；已知P、Q同时出发，以PQ为边作正方形PQMN，使正方形PQMN和△ABC在BC的同侧，设运动的时间为t秒（t≥0）．
（1）当点N落在AB边上时，t的值为，当点N落在AC边上时，t的值为；
（2）设正方形PQMN与△ABC重叠部分面积为S，求出当重叠部分为五边形时S与t的函数关系式以及t的取值范围；
（3）（本小题选做题，做对得5分，但全卷不超过150分）
如图2，分别取AB、AC的中点E、F，连接ED、FD，当点P、Q开始运动时，点G从BE中点出发，以每秒
个单位的速度沿折线BE－ED－DF向F点运动，到达F点停止运动．请问在点P的整个运动过程中，点G可能与PN边的中点重合吗？如果可能，请直接写出t的值或取值范围；若不可能，请说明理由．
如图所示，已知二次函数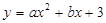
经过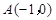
、
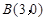、C三点，点
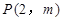是抛物线与直线
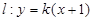的一个交点．
（1）求二次函数关系式和点C的坐标；
（2）对于动点
，求
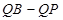的最大值；
（3）若动点M在直线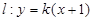上方的抛物线运动，过点M做x轴的垂线交x轴于点F，如果直线AP把线段MF分成1:2的两部分，求点M的坐标。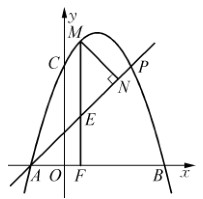
如图，⊙M与x轴相切于点C，与y轴的一个交点为A。
（1）求证：AC平分∠OAM；
（2）如果⊙M的半径等于4，∠ACO=300，求AM所在直线的解析式．