(本小题满分15分)
已知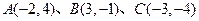 且
且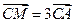 ,
,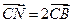 ,
,
求点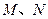 及
及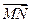 的坐标.
的坐标.
(本小题满分12分)
如图,在几何体P-ABCD中,四边形ABCD为矩形,PA⊥平面ABCD,AB=PA=2.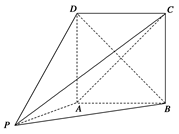
(1)当AD=2时,求证:平面PBD⊥平面PAC;
(2)若PC与AD所成角为45°,求几何体P-ABCD的体积.
(本小题满分12分)
(如右图) 在正方体ABCD-A1B1C1D1中,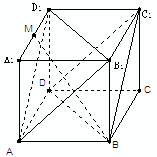
(1)证明:平面AB1D1∥平面BDC1
(2)设M为A1D1的中点,求直线BM与平面BB1D1D所成角的正弦值.
(本小题满分12分)
(1)若x>0,求函数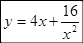 的最小值
的最小值
(2)设0<x<1,求函数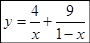 的最小值
的最小值
(本小题满分10分)已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.
已知函数
(1)求 的单调递减区间;
的单调递减区间;
(2)若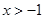 ,证明:
,证明: .
.