如图甲所示,在一个正方形金属线圈区域内,存在着磁感应强度B随时间变化的匀强磁场,磁场的方向与线圈平面垂直。金属线圈所围的面积S=200cm2,匝数n=1000,线圈电阻r=1.0Ω。线圈与电阻R构成闭合回路,电阻R=4.0Ω。匀强磁场的磁感应强度随时间变化的情况如图19乙所示,求:
(1)在t=2.0s时刻,通过电阻R的感应电流的大小;
(2)在t=2.0s时刻,电阻R消耗的电功率;
(3)0~6.0s内整个闭合电路中产生的热量。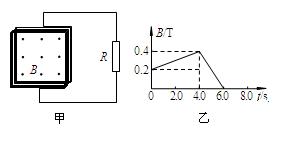
一列横波在x轴上传播,t1=0和t2="0.005" s时的波形,如图所示的实线和虚线.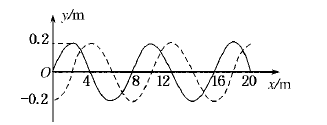
(1)设周期大于(t2-t1),求波速.
(2)设周期小于(t2-t1),并且波速为6000 m/s.求波的传播方向.
有两列简谐横波a、b在同一媒质中沿x轴正方向传播,波速均为v=2.5 m/s.在t=0时,两列波的波峰正好在x="2.5" m处重合,如图所示: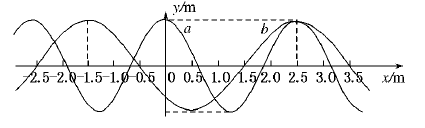
(1)求两列波的周期Ta和Tb.
(2)求t=0时,两列波的波峰重合处的所有位置.
如图所示,一列沿x轴正方向传播的简谐横波,波速大小为0.6 m/s,P点的横坐标为96 cm.从图中状态开始计时,问: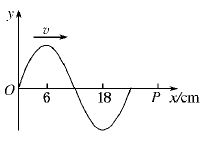
(1)经过多长时间,P质点开始振动?振动时方向如何?
(2)经过多长时间,P质点第一次到达波峰?
如图所示,两个光滑的定滑轮的半径很小,表面粗糙的斜面固定在地面上,斜面的倾角为θ=30°.用一根跨过定滑轮的细绳连接甲、乙两物体,把甲物体放在斜面上且连线与斜面平行,把乙物体悬在空中,并使悬线拉直且偏离竖直方向α=60°.现同时释放甲、乙两物体,乙物体将在竖直平面内振动,当乙物体运动经过最高点和最低点时,甲物体在斜面上均恰好未滑动.已知乙物体的质量为m=1 kg,若取重力加速度g=10 m/s2.求:甲物体的质量及斜面对甲物体的最大静摩擦力.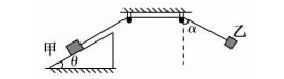
将一根一端固定的钢锯条自由端挨着圆盘踞的边缘,圆盘上均匀分布着50个齿,求:
(1)当它以10 r/s的转速转动时,钢锯条的振动周期为多少?
(2)当它以6 r/s的转速旋转时,发现钢锯条的振幅最大,可知钢锯条的固有频率是多少?(假定圆盘锯齿始终不脱离钢锯条)