计算: 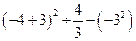
阅读:对于关于 的二次三项式
的二次三项式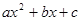 (
(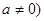 ,当
,当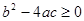 时,
时,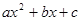 在实数范围内可以分解因式。
在实数范围内可以分解因式。
例:对于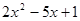 ,因为:
,因为: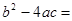
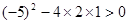 ,所以:
,所以: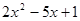 在实数范围内可以分解因式。
在实数范围内可以分解因式。
问题:当m取什么值的时候,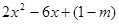 在实数范围内可以分解因式。
在实数范围内可以分解因式。
如图所示,已知:⊿ABC∽⊿DAC,AD=2,AC=4,BC=6,∠B=36°,∠D=117°,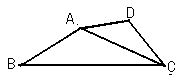
(1)求AB的长;
(2)求CD的长;
(3)求∠BAD的大小。
.画出⊿ABC以点P为位似中心的位似图形且⊿ABC与 ⊿A'B'C'的位似比是2∶1。
(1)分解因式
(2)解不等式组,并在数轴上表示解集: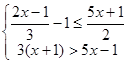
光华家农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区,两地区与该农机租赁公司商定每天的租赁价格如下表:
| 每台甲型收割机租金 |
每台乙型收割机租金 |
|
| A地区 |
1800元 |
1600元 |
| B地区 |
1600元 |
1200元 |
(1) 设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x的函数关系式,并写出x的取值范围;
(2) 若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案。并将各种方案设计出来;
(3) 如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提出一条合理建议。