质谱仪的工作原理图如图所示，A为粒子加速器，加速电压为U1：M为速度选择器，两板问有相互垂直的匀强磁场和匀强电场，匀强磁场的磁感应强度为B，，两板间距离为d；N为偏转分离器，内部有与纸面垂直的匀强磁场，磁感应强度为B2。一质量为m，电荷量为q的带正电的粒子由静止经加速器加速后，恰能通过速度选择器，进入分离器后做圆周运动，并打到感光板P上。不计重力，求：
（1）粒子经粒子加速器A加速后的速度”的大小及速度选择器肘两板间的电压以；
（2）粒子在偏转分离器Ⅳ的磁场中做圆周运动的半径尺：
（3）某同学提出：在其它条件不变的情况下，只减小加速电压U。，就可以使粒子在偏转分离器Ⅳ的磁场中做圆周运动的半径减小。试分析他的说法是否正确。
素有“陆地冲浪”之称的滑板运动已深受广大青少年喜爱．如图所示是由足够长的斜直轨道，半径R1＝2 m的凹形圆弧轨道和半径R2＝3.6 m的凸形圆弧轨道三部分组成的模拟滑板组合轨道．这三部分轨道依次平滑连接，且处于同一竖直平面内．其中M点为凹形圆弧轨道的最低点，N点为凸形圆弧轨道的最高点，凸形圆弧轨道的圆心O与M点在同一水平面上．一可视为质点，质量为m＝1 kg的滑板从斜直轨道上的P点无初速度滑下，经M点滑向N点，P点距水平面的高度h＝3.2 m，不计一切阻力，g取10 m/s2．求：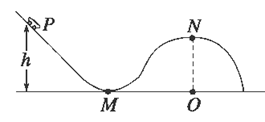
（1）滑板滑至M点时的速度；
（2）滑板滑至M点时，轨道对滑板的支持力；
（3）若滑板滑至N点时对轨道恰好无压力，则滑板的下滑点P距水平面的高度．
如图所示，一质量为M=2kg的铁锤从距地面h=3.2m处自由下落，恰好落在地面上的一个质量为m=6kg的木桩上，随即与木桩一起向下运动，经时间t=0.1s停止运动。求木桩向下运动时受到地面的平均阻力大小。（铁锤的横截面小于木桩的横截面，木桩露出地面部分的长度忽略不计，重力加速度g=10m/s2）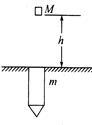
在折射率为n，厚度为d的玻璃平板上方的空气中有一点光源S，从S发出的光线SA以入射角θ 入射到玻璃板上表面，经过玻璃板后从下表面射出，如图所示。若沿此光线传播的光从光源 S 到玻璃板上表面的传播时间与在玻璃板中传播时间相等，点光源S到玻璃板上表面的垂直距离l应是多少？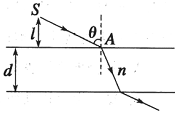
容器内装有1kg的氧气，开始时，氧气压强为1.0×106Pa，温度为57℃，因为漏气，经过一段时间后，容器内氧气压强变为原来的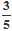
，温度降为27℃，求漏掉多少千克氧气？
如图所示，AB是倾角为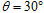
的粗糙直轨道，BCD是光滑的圆弧轨道，AB恰好在B点与圆弧相切，圆弧的半径为R，一个质量为m的物体（可以看做质点）从直轨道上的P点由静止释放，结果它能在两轨道间做往返运动。已知P点与圆弧的圆心O等高，物体与轨道AB间的动摩擦因数为μ。求：
（1）物体做往返运动的整个过程中在AB轨道上通过的总路程；
（2）最终当物体通过圆弧轨道最低点E时，对圆弧轨道的压力；
（3）为使物体能顺利到达圆弧轨道的最高点D，释放点距B点的距离L′至少多大。