(本小题满分14分)
已知数列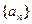 ,
,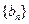 满足
满足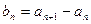 ,其中
,其中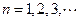 .
.
(Ⅰ)若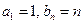 ,求数列
,求数列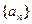 的通项公式;
的通项公式;
(Ⅱ)若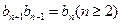 ,且
,且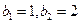 .
.
(ⅰ)记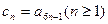 ,求证:数列
,求证:数列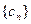 为等差数列;
为等差数列;
(ⅱ)若数列 中任意一项的值均未在该数列中重复出现无数次. 求首项
中任意一项的值均未在该数列中重复出现无数次. 求首项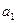 应满足的条件.
应满足的条件.
(1)求 的值.
的值.
(2)若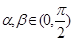 ,
, ,
,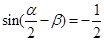 ,求
,求 的值.
的值.
已知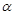 ∈(0,
∈(0,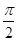 ),且
),且 ,
,
求 的值.
的值.
已知函数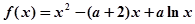 ,其中常数
,其中常数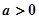 。
。
(1)当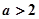 时,求函数
时,求函数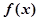 的单调递增区间;
的单调递增区间;
(2)当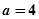 时,是否存在实数
时,是否存在实数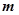 ,使得直线
,使得直线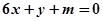 恰为曲线
恰为曲线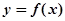 的切线?若存在,求出
的切线?若存在,求出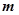 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)设定义在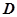 上的函数
上的函数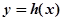 的图象在点
的图象在点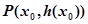 处的切线方程为
处的切线方程为 ,当
,当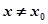 时,若
时,若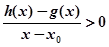 在
在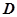 内恒成立,则称
内恒成立,则称 为函数
为函数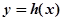 的“类对称点”。当
的“类对称点”。当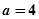 ,试问
,试问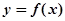 是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
已知数列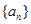 中,
中, ,
,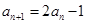 (
( )
)
(1)求数列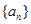 的通项公式;
的通项公式;
(2)设 ,数列
,数列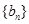 的前
的前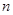 项和为
项和为 ,求证:
,求证:  .
.
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为 m,
m, m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕
m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕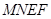 ,
, .线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
(1)求S关于x的函数关系式及该函数的定义域;
(2)当x取何值时,液晶广告屏幕MNEF的面积S最小?