如图,在锐角三角形ABC中,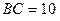 ,BC边上的高AM=6,D,E分别是边AB,AC上的两个动点(D不与
,BC边上的高AM=6,D,E分别是边AB,AC上的两个动点(D不与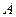 ,
,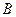 重合),且保持DE∥BC,以DE为边,在点
重合),且保持DE∥BC,以DE为边,在点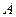 的异侧作正方形DEFG.
的异侧作正方形DEFG. 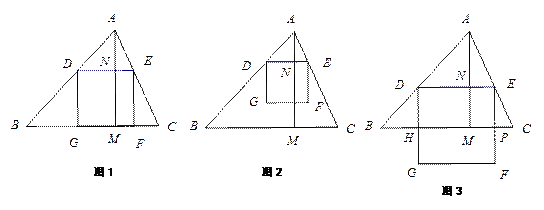
(1)因为 ,所以△ADE∽△ABC.
(2)如图1,当正方形DEFG的边GF在BC上时,求正方形DEFG的边长;
(3)设DE = x,△ABC与正方形DEFG重叠部分的面积为y.
①如图2,当正方形DEFG在△ABC的内部时,求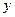 关于
关于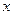 的函数关系式,写出x的取值范围;
的函数关系式,写出x的取值范围;
②如图3,当正方形DEFG的一部分在△ABC的外部时,求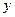 关于
关于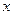 的函数关系式,写出x的取值范围;
的函数关系式,写出x的取值范围;
③当x为何值时,y有最大值,最大值是多少?
九(1)班数学课题学习小组,为了研究学习二次函数问题,他们经历了实践——应用——探究的过程
(1)实践:他们对一条公路上横截面为抛物线的单向双车道的隧道进行测量,测得隧道的路面宽为10米,隧道顶部最高处距地面6.25米,并画出了隧道截面图,建立了如图所示的直角坐标系,请你求出抛物线的解析式
(2)应用:按规定机动车辆通过隧道时,车顶部与隧道顶部在竖起方向上的高度差至少为0.5米,为了确保安全,问该隧道能否让最宽3米,最高3.5米的两辆车居中并列行驶(不考虑两车之间的空隙)?
(3)探究:该课题学习小组为进一步探究抛物线的有关知识,他们借助上述抛物线模型,提出了以下两个问题,请予解答:
①如图,在抛物线内作矩形ABCD,使顶点C、D落在抛物线上,顶点A、B落在x轴上,设矩形ABCD的周长为为l,求l的最大值
②如图,过原点作一条直线y=x,交抛物线于M,交抛物线的对称轴于N,P为直线OM上一动点,过点P作x轴的垂线交抛物线于点Q,问在直线OM上是否存在点P,使以点P、N、Q为顶点的三角形为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由
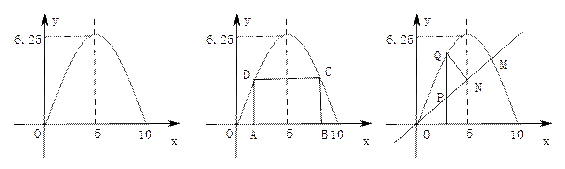 |
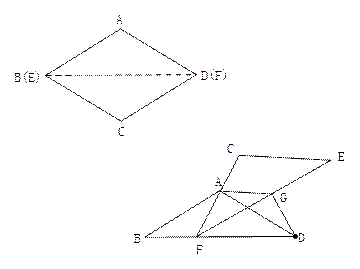
如图①,将菱形纸片AB(E)CD(F)沿对角线BD(EF)剪开,得到△ABD和△ECF,固定△ABD,并把△ABD与△ECF叠放在一起
(1)操作:如图②,将△ECF的顶点F固定在△ABD的BD边上的中点处,将△ECF绕点F在BD的上方左右旋转,设旋转时FC交BA于H(不与点B重合),EF交DA于G(不与点D重合),求证:BH·GD=BF2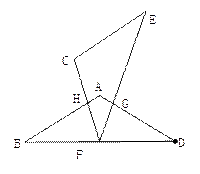 (2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(不与点B、D重合),且CF如终过点A,过点A作AG∥CE,交EF于G,连接DG
(2)操作:如图③,△ECF的顶点F在△ABD的BD边上滑动(不与点B、D重合),且CF如终过点A,过点A作AG∥CE,交EF于G,连接DG
探究:FD+DG=,并请证明你的结论
 |
某工厂有一种材料,可加工甲、乙、丙三种型号机械配件共240件,厂方计划由20个工人一天内加工完成,并要求每人只加工一种配件,根据下表提供的信息,解答下列问题:
| 配件种类 |
甲 |
乙 |
丙 |
| 每人可加工配件的数量(个) |
16 |
12 |
10 |
| 每个配件获利(元) |
6 |
8 |
5 |
(1)设加工甲种配件的人数为x,加工乙种配件的人数为y,求y与x之间的函数关系式
(2)如果加工每种配件的人数均不少于3人,那么加工配件的人数安排方案有几种?并写出每种安排方案
(3)要使此次加工配件的利润最大,应采用哪种方案?最大利润是多少?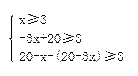
已知⊙O的直径AB的长为4㎝,C是⊙O上一点,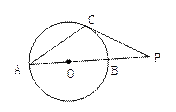 ∠BAC=30°,过点C作⊙O的切线交AB的延长线于点
∠BAC=30°,过点C作⊙O的切线交AB的延长线于点
P,求BP的长
根据国务院新闻办公室2011年4月28日发布的《2011年全国第六次人口普查主要数据公报(第1号)》,就全国人口受教育情况的数据绘制了条形统计图和扇形统计图如下: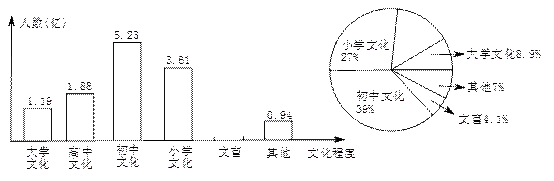
根据统计图提供的信息,解答下列问题:
(1)这次人口普查统计的全国人口总数约为亿人(精确到0.1)
(2)补全条条形统计图和扇形统计图
(3)求扇形统计图中表示“高中文化”的圆心角的度数