一质量为M =" 0.8" kg的中空的、粗细均匀的、足够长的绝缘细管，其内表面粗糙、外表面光滑；有一质量为m =" 0.2" kg、电荷量为q =" 0.1" C的带正电小滑块以水平向右的速度进入管内，如图甲。细管置于光滑的水平地面上，细管的空间能让滑块顺利地滑进去，示意图如图乙。运动过程中滑块的电荷量保持不变。空间中存在垂直纸面向里的水平匀强磁场，磁感强度为B =" 1.0" T。（取水平向右为正方向，g =" 10" m/s2）
(1)滑块以v0 = 10 m/s的初速度进入管内，则系统最终产生的内能为多少?
(2)滑块最终的稳定速度 vt取决于滑块进入细管时的初速度v0，请以滑块的初速度v0为横坐标、滑块最终稳定时的速度vt 为纵坐标，在丙图中画出滑块的vt—v0图象（只需画出v0的取值范围在0至60 m/s的图象）。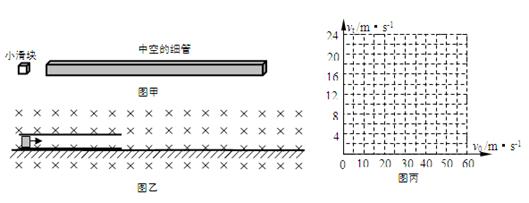
一斜面AB长为10m，倾角为30°，一质量为2kg的小物体（大小不计）从斜面顶端A点由静止开始下滑，如图所示（g取10 m/s2）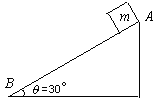
若斜面与物体间的动摩擦因数为0.5，求小物体下滑到斜面底端B点时的速度及所用时间．
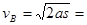3.65m/s
s若给小物体一个沿斜面向下的初速度，恰能沿斜面匀速下滑，则小物体与斜面间的动摩擦因数μ是多少? μ＝0.58
一质点做匀加速直线运动，初速度为10m/s ，加速度为2m/s2 。试求该质点：第5s末的速度20 m/s
前5s内的平均速度15m/s
第5s内的平均速度19m/s
吴菊萍徒手勇救小妞妞，被誉为“最美妈妈”．设妞妞的质量m=10kg，从离地h= 28．5m高的阳台掉下，下落过程中空气阻力约为本身重力的0.4倍；在妞妞开始掉下时，吴菊萍立刻从静止开始匀加速奔跑水平距离s =9m到达楼下，恰好张开双臂在距地面高度为h2=1.5m处接住妞妞，缓冲到地面时速度为零，缓冲过程中的空气阻力不计。g取10m／s2，求：
妞妞在被接到前下落的时间．
吴菊萍跑到楼下时的速度．
在缓冲过程中吴菊萍对妞妞做的功．
如图所示，用两根轻绳和一根轻弹簧将质量均为m的A、B两小球以及水平天花板上的固定点O之间两两连接，然后用一水平方向的恒力作用于A球上，此时两根轻绳均处于直线状态，且OB绳恰好处于竖直方向，两球均处于静止状态。已知三段长度之比为OA：AB：OB =3：4：5，重力加速度为g 。试确定：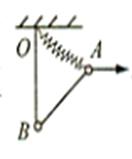
弹簧OA的拉力．
若突然将恒力撤去，则撤去瞬间，小球A的加速度．
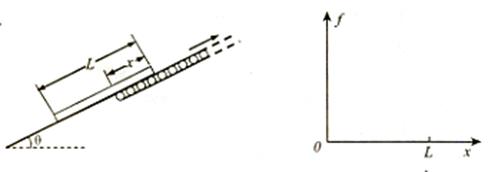
如图所示，一块长为L、质量m的扁平均匀规则木板通过装有传送带的光滑斜面输送，斜面与传送带靠在一起并与传送带上表面连成一直线，与水平方向夹角为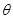
，传送带以较大的恒定速率转动，传送方向向上，木板与传送带之间动摩擦因数为常数，已知木板放在斜面或者传送带上任意位置时，支持力均匀作用在木板底部，将木板静止放在传送带和光滑斜面之间某一位置，位于传送带部位的长度设为x，当
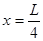时，木板能保持静止。设传送带与木板间产生的滑动摩擦力为f，试在0≤x≤L范围内，画出f—x图象．（本小题仅根据图象给分）
木板从
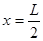的位置静止释放，当移动到x=L的位置时，木板的速度多大？在（2）的过程中，木块的机械能增加量设为△E，传送带因运送木板而多消耗的电能设为w，试比较△E和w的大小关系，用文字说明理由。
