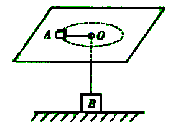
如图所示 ,粗糙斜面与光滑水平面通过半径可忽略的光滑小圆弧平滑连接,斜面倾角 θ = 37°,A、C、D滑块的质量为 mA= mC= mD=" m" =" 1" kg,B滑块的质量 mB =" 4" m =" 4" kg(各滑块均视为质点 )。A、B间夹着质量可忽略的火药。K为处于原长的轻质弹簧,两端分别连接住B和C。现点燃火药(此时间极短且不会影响各物体的质量和各表面的光滑程度),此后,发现A与D相碰后粘在一起,接着沿斜面前进了L =" 0.8" m 时速度减为零,此后设法让它们不再滑下。已知滑块A、D与斜面间的动摩擦因数均为 μ = 0.5,取 g = 10 m/s2,sin37°= 0.6,cos37°= 0.8。求:
)。A、B间夹着质量可忽略的火药。K为处于原长的轻质弹簧,两端分别连接住B和C。现点燃火药(此时间极短且不会影响各物体的质量和各表面的光滑程度),此后,发现A与D相碰后粘在一起,接着沿斜面前进了L =" 0.8" m 时速度减为零,此后设法让它们不再滑下。已知滑块A、D与斜面间的动摩擦因数均为 μ = 0.5,取 g = 10 m/s2,sin37°= 0.6,cos37°= 0.8。求:
(1)火药炸完瞬间A的速度vA;
(2)滑块B、C和弹簧K构成的系统在相互作用过程 中,弹簧的最大弹性势能Ep。(弹簧始终未超出弹性限度)。
中,弹簧的最大弹性势能Ep。(弹簧始终未超出弹性限度)。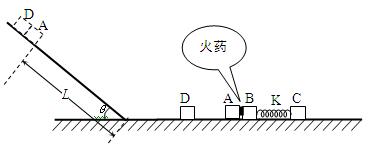
处在激发态的氢原子向能量较低的状态跃迁时会发出一系列不同频率的光,称为氢光谱.氢光谱线的波长可以用下面的巴耳末—里德伯公式来表示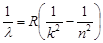
n,k分别表示氢原子跃迁前后所处状态的量子数.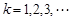 ,对于每一个k,有
,对于每一个k,有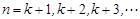 ,R称为里德伯常量,是一个已知量.对于
,R称为里德伯常量,是一个已知量.对于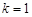 的一系列谱线其波长处在紫外线区,称为赖曼系;
的一系列谱线其波长处在紫外线区,称为赖曼系;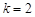 的一系列谱线其波长处在可见光区,称为巴耳末系.
的一系列谱线其波长处在可见光区,称为巴耳末系.
用氢原子发出的光照射某种金属进行光电效应实验,当用赖曼系波长最长的光照射时,遏止电压的大小为U1,当用巴耳末系波长最短的光照射时,遏止电压的大小为U2. 已知电子电量的大小为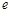 ,真空中的光速为
,真空中的光速为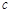 ,试求:普朗克常量和该种金属的逸出功.
,试求:普朗克常量和该种金属的逸出功.
一木块位于光滑的水平桌面上,木块上固定一支架。木块与支架的总质量为M,一摆球挂于支架上,摆球质量为m,m<(1/2)M。摆线的质量不计,初始时,整个装置处于静止,现有一颗质量也为m子弹以速率V0水平射入摆球并立即停留在球内,摆球与子弹便一起运动,已知摆球摆起的最大的角度小于90度。运动过程中支架不会倾倒。
求:1.摆球上升的最大高度 ? 2.木块运动过程中的最大速率?3.摆球在最低处的速度大小和方向?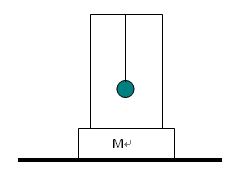
太阳现正处于主序星演化阶段。它主要是由电子和 、
、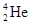 等原子核组成。维持太阳辐射的是它内部的核聚变反应,核反应方程是
等原子核组成。维持太阳辐射的是它内部的核聚变反应,核反应方程是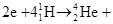 释放的核能,这些核能最后转化为辐射能。根据目前关于恒星演化的理论,若由于聚变反应而使太阳中的
释放的核能,这些核能最后转化为辐射能。根据目前关于恒星演化的理论,若由于聚变反应而使太阳中的 核数目从现有数减少10%,太阳将离开主序星阶段而转入红巨星的演化阶段。为了简化,假定目前太阳全部由电子和
核数目从现有数减少10%,太阳将离开主序星阶段而转入红巨星的演化阶段。为了简化,假定目前太阳全部由电子和 核组成。
核组成。
(1)为了研究太阳演化进程,需知道目前太阳的质量M。已知地球半径R=6.4×106 m,地球质量m=6.0×1024 kg,日地中心的距离r=1.5×1011 m,地球表面处的重力加速度 g=10 m/s2,1年约为3.2×107秒,试估算目前太阳的质量M。
(2)已知质子质量mp=1.6726×10-27 kg,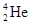 质量mα=6.6458×10-27 kg,电子质量 me=0.9×10-30 kg,光速c=3×108 m/s。求每发生一次题中所述的核聚变反应所释放的核能。
质量mα=6.6458×10-27 kg,电子质量 me=0.9×10-30 kg,光速c=3×108 m/s。求每发生一次题中所述的核聚变反应所释放的核能。
(3)又知地球上与太阳垂直的每平方米截面上,每秒通过的太阳辐射能w=1.35×103 W/m2。试估算太阳继续保持在主序星阶段还有多少年的寿命。(估算结果只要求一位有效数字。)
如图所示,长为R的不可伸长轻绳上端固定在O点,下端连接一小球,小球与地面间的距离可以忽略(但小球不受地面支持力)且处于静止状态.在最低点给小球一沿水平方向的初速度,此时绳子恰好没断,小球在竖直平面内做圆周运动。假设小球到达最高点时由于绳子碰到正下方P处的钉子恰好断裂,最后小球落在距初始位置水平距离为4R的地面上,重力加速度为g.试求: 
(1)绳突然断开时小球的速度v;
(2)竖直方向上O与P的距离L.
如图所示,细绳一端系着质量m="0.1" kg的小物块A,置于光滑水平台面上;另一端通过光滑小孔O与质量M="0.5" kg的物体B相连,B静止于水平地面上。当A以O为圆心做半径r =0.2m的匀速圆周运动时,地面对B的支持力F =3.0N,求物块A的速度ν和角速度ω的大小。(g=10m/s2)