如图11所示，一根长0.1 m的细线，一端系着一个质量为0.18 kg的小球，拉住线的另一
端，使小球在光滑的水平桌面上做匀速圆周运动。当小球的转速改为原来的3倍时，细线将恰好会断开，线断开前的瞬间，小球受到的拉力比原来的拉力大40 N，求：
（1）线断开前的瞬间，线受到的拉力大小？
（2）线断开的瞬间，小球运动的线速度？
（3）如果小球离开桌面时，速度方向与桌边缘的夹角为60°，桌面高出地面0.8 m，求小球飞出后的落地点距桌边缘的水平距离？（取g = 10m/s2）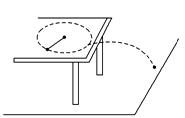
一辆汽车从原点O由静止出发沿x轴做直线运动，为研究汽车的运动而记下它在各时刻的位置和速度，见下表，求
| 时刻t/s |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 位置的坐标x/m |
0 |
0.5 |
2 |
4.5 |
8 |
12 |
16 |
20 |
| 瞬时速度v/(m·s－1) |
1 |
2 |
3 |
4 |
4 |
4 |
4 |
4 |
(1)汽车在第2s末的瞬时速度为多少？
(2)汽车在前3s内的加速度为多少？
(3)汽车在第4s内的平均速度为多少？
(4)汽车在前4s内的平均速度为多少？
如图所示，倾角为30°的光滑斜面与粗糙的水平面平滑连接。现将一滑块（可视为质点）从斜面上A点由静止释放，最终停在水平面上的C点。已知A点距水平面的高度h=0.8m，B点距C点的距离L=2.0m。（滑块经过B点时没有能量损失，g=10m/s2），求：
（1）滑块在运动过程中的最大速度；
（2）滑块与水平面间的动摩擦因数μ；
（3）滑块从A点释放后，经过时间t=1.0s时速度的大小。
(10分)如图，有一水平传送带以2m/s的速度匀速运动，现将一物体轻轻放在传送带上，若物体与传送带间的动摩擦因数为0.5，则传送带将该物体传送10m的距离所需时间为多少？(g=10m/s2)
如图所示，质量为
的纸箱在推力F的作用下沿水平地面运动，推力
，方向与水平面的夹角为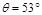
，纸箱与水平地面的动摩擦因数为
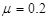。（取
，
，
），
求：（1）求纸箱的加速度大小。
（2）纸箱由静止开始运动，第
内的位移多大?
质量为2kg的物体在水平推力F的作用下沿水平面做直线运动，一段时间后撤去F，其运动的v-t图像如图所示。求：（重力加速度g＝10m/s2）
（1）物体与水平面间的动摩擦因数m；
（2）水平推力F的大小；