如图,在同一平面内,将两个全等的等腰直角 和
和 摆放在一起,
摆放在一起, 为公共顶点,
为公共顶点,
 ,它们的斜边长为2,若
,它们的斜边长为2,若 固定不动,
固定不动, 绕点
绕点 旋转,
旋转, 、
、 与边
与边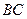 的交点分别为
的交点分别为 、
、 (点
(点 不与点
不与点 重合,点
重合,点 不与点
不与点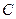 重合),设
重合),设 ,
, .
.
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对加以证明.
(2)求 与
与 的函数关系式,直接写出自变量
的函数关系式,直接写出自变量 的取值范围.
的取值范围.
在一个不透明的口袋里装有分别标注2、4、6的3个小球(小球除数字外,其余都相同),另有3张背面完全一样、正面分别写有数字6、7、8的卡片.现从口袋中任意摸出一个小球,再从这3张背面朝上的卡片中任意摸出一张卡片.
(1)请你用列表或画树状图的方法,表示出所有可能出现的结果;
(2)小红和小莉做游戏,制定了两个游戏规则:
规则1:若两次摸出的数字,至少有一次是“6”,小红赢;否则,小莉赢.
规则2:若摸出的卡片上的数字是球上数字的整数倍时,小红赢;否则,小莉赢.
小红想要在游戏中获胜机会更大些,她会选择哪一条规则,并说明理由.
过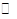 O上一点M作弦MA、MB、MC,使∠AMB=∠BMC,过B作BE⊥MA于E,BF⊥MC于F,求证:AE=CF.
O上一点M作弦MA、MB、MC,使∠AMB=∠BMC,过B作BE⊥MA于E,BF⊥MC于F,求证:AE=CF.
如图,在平面直角坐标系中,点A、B的坐标分别为(-1,3)、(-4,1),先将线段AB沿一确定方向平移得到线段A1B1,点A的对应点为A1,点B1的坐标为(0,2),再将线段A1B1绕原点O顺时针旋转90°得到线段A2B2,点A1的对应点为点A2.
(1)画出线段A1B1、A2B2;
(2)直接写出点A1到达点A2所经过的路径长.
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(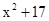 )cm,正六边形的边长为(
)cm,正六边形的边长为( )cm
)cm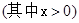 .求这两段铁丝的总长.
.求这两段铁丝的总长.
解方程:x2-4x+1=0