如图所示,把球夹在竖直墙壁AC和木板BC之间,不计摩擦,设球对墙壁的压力大小为F1,对木板的压力大小为F2,现将木板BC缓慢转至水平位置的过程中( )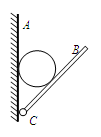
| A.F1、F2都增大 | B.F1增加、F2减小 |
| C.F1减小、F2增加 | D.F1、F2都减小 |
如图所示,分别在M、N两点固定放置两个点电荷+Q和-q (Q>q) ,以MN连线的中点O为圆心的圆周上有四点A、B、C、D,关于这四点的场强和电势,下列说法中正确的是()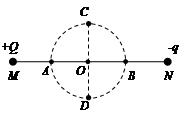
A.A点电势高于B点电势
B.A点场强小于B点场强
C.C点电势低于D点电势
D.C点场强大于D点场强
两个可以自由移动的点电荷分别放在A、B两处,如图1所示,A处电荷带正电Q1,B处电荷带负电Q2,且Q2 = 4Q1,另取一个可以自由移动的点电荷Q3,放在AB直线上,欲使整个系统处于平衡状态,则()
A.Q3为正电荷,且放于A左方
B.Q3为负电荷,且放于B右方
C.Q3为负电荷,且放于AB之间
D.Q3为正电荷,且放于B右方
如图所示, A、B两物体叠放在水平地面上,在水平力F的作用下一起向右做匀速运动,若将水平力F作用在A上,两物体可能发生的情况是()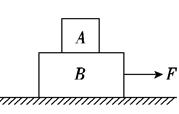
A.A、B一起匀速运动
B.A加速运动,B匀速运动
C.A加速运动,B静止
D.A与B一起加速运动
如图甲所示,在倾角为θ的光滑斜面上,有一个质量为m的物体在沿斜面方向的力F的作用下由静止开始运动,物体的机械能E随位移x的变化关系如图乙所示。其中0~x1过程的图线是曲线,x1~x2过程的图线为平行于x轴的直线,则下列说法中正确的是()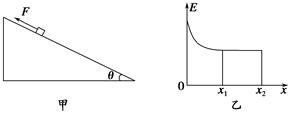
| A.物体在沿斜面向下运动 |
| B.在0~x1过程中,物体的加速度一直减小 |
| C.在0~x2过程中,物体先减速再匀速 |
| D.在x1~x2过程中,物体的加速度为gsinθ |
一个用半导体材料制成的电阻器D,其电流I随它两端的电压U的关系图象如图甲所示,将它与两个标准电阻R1、R2并联后接在电压恒为U的电源上,如图乙所示,三个用电器消耗的电功率均为P。现将它们连接成如图丙所示的电路,仍然接在该电源的两端,设电阻器D和电阻R1、R2消耗的电功率分别为PD、P1、P2,它们之间的大小关系为()
| A.P1=4P2 | B.PD<P2 |
| C.P1>4P2 | D.PD>P2 |