如图所示,坐标空间中有场强为E的匀强电场,和磁感应强度为B的匀强磁场,Y轴为两种场的分界线,图中虚线为磁场区域的右边界,现有一质量为m,电荷量为-q的带电粒子从电场中坐标位置(-L,O)处,以初速度V0沿X轴正方向开始运动,且已知L=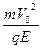 (重力不计)。试求:(1)带电粒子进入磁场时速度的大小?
(重力不计)。试求:(1)带电粒子进入磁场时速度的大小?
(2)若要使带电粒子能穿越磁场区域而不再返回电场中,磁场的宽度d应满足的条件?
如题图所示,在半径为a的圆柱空间中(图中圆为其横截面)充满磁感应强度大小为B的均匀磁场,其方向平行于轴线远离读者.在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为L=1.6a的刚性等边三角形框架ΔDEF,其中心O位于圆柱的轴线上.DE边上S点(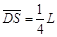 )处有一发射带电粒子的源,发射粒子的方向皆在题图中截面内且垂直于DE边向下。发射粒子的电量皆为q(>0),质量皆为m,但速度v有各种不同的数值。若这些粒子与三角形框架的碰撞无能量损失(不能与圆柱壁相碰),电量也无变化,且每一次碰撞时速度方向均垂直于被碰的边。试问:
)处有一发射带电粒子的源,发射粒子的方向皆在题图中截面内且垂直于DE边向下。发射粒子的电量皆为q(>0),质量皆为m,但速度v有各种不同的数值。若这些粒子与三角形框架的碰撞无能量损失(不能与圆柱壁相碰),电量也无变化,且每一次碰撞时速度方向均垂直于被碰的边。试问: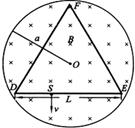
(1)带电粒子经多长时间第一次与DE边相碰?
(2)带电粒子速度v的大小取哪些数值时可使S点发出的粒子最终又回到S点?
(3)这些粒子中,回到S点所用的最短时间是多少?
一个质量m=0.1g的小滑块,带有q=5×10-4C的电荷放置在倾角 α=30°光滑斜面上(绝缘),斜面置于B=0.5T的匀强磁场中,磁场方向垂直纸面向里,如图所示,小滑块由静止开始沿斜面滑下,其斜面足够长,小滑块滑至某一位置时,要离开斜面。(g=10m/s2)求: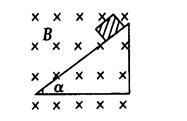
(1)小滑块带何种电荷?
(2)小滑块离开斜面的瞬时速度多大?
(3)该斜面的长度至少多长?
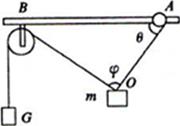
如图所示,细绳OA的O端与质量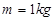 的重物相连,A端与轻质圆环(重力不计)相连,圆环套在水平棒上可以滑动;定滑轮固定在B处,跨过定滑轮的细绳,两端分别与重物m、重物G相连,若两条细绳间的夹角
的重物相连,A端与轻质圆环(重力不计)相连,圆环套在水平棒上可以滑动;定滑轮固定在B处,跨过定滑轮的细绳,两端分别与重物m、重物G相连,若两条细绳间的夹角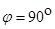 ,OA与水平杆的夹角
,OA与水平杆的夹角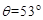 圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,滑动摩擦力等于最大静摩擦力.(已知
圆环恰好没有滑动,不计滑轮大小,整个系统处于静止状态,滑动摩擦力等于最大静摩擦力.(已知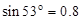 ;
;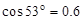 ):
):
(1)圆环与棒间的动摩擦因数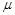 ;
;
(2)重物G的质量M
如图,质量分别为mA、mB的两个弹性小球A、B静止在地面上方,B球距离地面的高度h=0.8m,A球在B球的正上方。先将B球释放,经过一段时间后再将A球释放。当A球下落t=0.3s时,刚好与B球在地面上方的P点处相碰,碰撞时间极短,碰后瞬间A球的速度恰好为零。已知mB=3mA,重力加速度大小g=10m/s2,忽略空气阻力及碰撞中的动能损失。求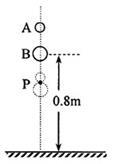
(1)B球第一次到达地面时的速度;
(2)P点距离地面的高度。
如图所示,平行玻璃板的厚度d=4cm,光线AB以入射角θ1=60°从空气射到平行玻璃板的上表面,经两次折射后从玻璃板的下表面射出。已知玻璃的折射率n=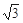 。求出射光线CD相对于入射光线AB偏离的距离δ。
。求出射光线CD相对于入射光线AB偏离的距离δ。