当物体从高空下落时，空气阻力（不计空气的浮力）会随物体的速度增大而增大，因此经过一段距离后将匀速下落，这个速度称为此物体下落的终极速度．研究发现，在相同环境条件下，球形物体的终极速度仅与球的半径和质量有关．（g取10m/s2）下表是某次研究的实验数据：
| 小球编号 |
A |
B |
C |
| 小球的半径（×10-2m） |
0.5 |
0.5 |
1.5 |
| 小球的质量（×10-3kg） |
2 |
5 |
45 |
| 小球的终极速度（m/s） |
16 |
40 |
40 |
（1）根据表中的数据，求出B球与C球在达到终极速度时所受的空气阻力之比fB∶fC．
（2）根据表中的数据，归纳出球型物体所受的空气阻力f与球的终极速度v及球的半径r的关系，写出表达式并求出比例系数．
质量为2 kg的物体放到水平地板上，用一轻弹簧水平拉该物体，物体由静止开始，开始 2 s 时间内，物体运动 2 m 位移，此过程中弹簧始终保持伸长3 cm，己知弹簧的劲度系数为 k ="100" N/m．求：物体和地板间的动摩擦因数．
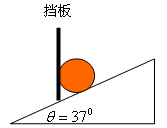
如图所示，一个质量为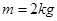
的均质小球放在倾角为
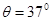的光滑斜面上，并被斜面上一个竖直的光滑挡板挡住，处于静止状态，试求小球对挡板和斜面的压力（已知
）
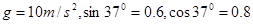在S点的电量为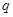
质量为
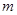的静止带电粒子被加速电压U，柜间距离为
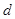的匀强电场加速后，从正中央垂直射入板间距离和板长度均为L，电压为U的匀强偏转电场偏转后，立即进入一个垂直纸面方面的匀强磁场，其磁感应强度为B，若不计重力影响，欲使带电粒子通过某距径返回S点，求：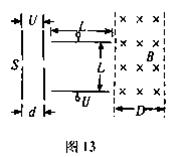
匀强磁场的宽度D至少多少？
该带电粒子周期T是多少？偏转电压正负极多长时间变换一次方向。
某校物理兴趣小组决定举行遥控赛车比赛。比赛路径如图所示，赛车从起点A出发，沿水平直线轨道运动L后，由B点进入半径为R的光滑竖直圆轨道，离开竖直圆轨道后继续在水平直轨道上运动L¢距离到C点，并能越过壕沟。已知赛车质量m=0．1kg，通电后以额定功率P=1．5W工作，在两段水平直轨道上受到阻力恒为0．2N。图中L=10．00m，L¢=2．00m，R=0．32m，h=1．25m，s=1．50m。问：要使赛车完成比赛，电动机至少工作多长时间？（取g=10m/s2）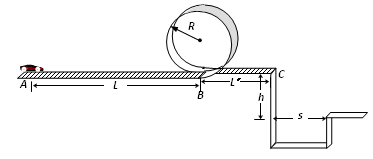
平行板电容大路两极板之间距离为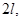
在中央有一块带电网，网与正极板B之间的电势差为网与负极板A之间电势差的2倍，从板A与水平成
角飞出一个带正电粒子，最高到达B板
处，求粒子起飞到返回A上点之间的距离。（重力作用不计）