如图甲所示，空间存在B ="0." 5T、方向
竖直向下的匀强磁场，MN、PQ是放在同一水平面内的平行长直导轨，其间距L =" 0.2m" ，R是连在导轨一端的电阻，ab是跨接在导轨上质量m =" 0.1" kg的导体棒，导体棒与轨道间的滑动摩擦系数为
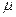=0.2。从零时刻开始，对ab施加一个方向水平向右的恒定拉力F，使其从静止开始沿导轨运
动，此过程中棒始终保持与导轨垂直且接触良好，图乙是棒的速度一时间关系图象，其中AO是图象在O点的切线，AB是图象的渐近线。（g取10m/s2， 除R以外，其余部分的电阻均不计）求：
（1）恒力F的大小为多少？
（2）当棒的速度达到
时，导体棒的加速度大小为多少？
（3）从0到6s这段时间内电阻上产生的热量为Q = 4.3J。求此过程中导体棒运动的位移S为多少？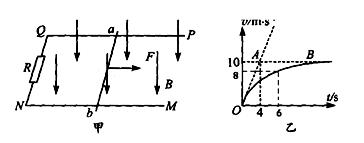
如图甲所示，在倾角为30°的足够长光滑斜面AB前，有一粗糙水平面OA，OA长为4 m．有一质量为m的滑块，从O处由静止开始受一水平向右的力F作用．F按图乙所示的规律变化．滑块与OA间的动摩擦因数μ＝0.25，g取10 m/s2，试求：
(1)滑块到A处的速度大小；
(2)不计滑块在A处的速率变化，滑块冲上斜面AB的长度是多少？
图为修建高层建筑常用的塔式起重机．在起重机将质量m＝5×104 kg的重物竖直吊起的过程中，重物由静止开始向上做匀加速直线运动，加速度a＝0.2 m/s2，当起重机输出功
率达到其允许的最大值时，保持该功率直到重物做vm＝1.02 m/s的匀速运动．取g＝10 m/s2，不计额外功．求：
(1)起重机允许输出的最大功率．
(2)重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率．
一辆汽车质量为1×103 kg，最大功率为2×104 W，在水平路面上由静止开始做直线运动，最大速度为v2，运动中汽车所受阻力恒定．发动机的最大牵引力为3×103 N，其行驶过程中牵引力F与车速的倒数
的关系如图所示．试求：
(1)根据图线ABC判断汽车做什么运动？
(2)v2的大小；
(3)整个运动过程中的最大加速度；
(4)匀加速运动过程的最大速度是多大？当汽车的速度为10 m/s时发动机的功率为多大？
月球自转一周的时间与月球绕地球运行一周的时间相等，都为T0.我国的“嫦娥二号”探月卫星于2010年10月成功进入绕月运行的“极月圆轨道”，这一圆形轨道通过月球两极上空，距月面的高度为h.若月球质量为m月，月球半径为R，引力常量为G.
(1)求“嫦娥二号”绕月运行的周期．
(2)在月球自转一周的过程中，“嫦娥二号”将绕月运行多少圈？
(3)“嫦娥二号”携带了一台CCD摄像机(摄像机拍摄不受光照影响)，随着卫星的飞行，摄像机将对月球表面进行连续拍摄．要求在月球自转一周的时间内，将月面各处全部拍摄下来，摄像机拍摄时拍摄到的月球表面宽度至少是多少？
宇航员在一行星上以10 m/s的初速度竖直上抛一质量为0.2 kg的物体，不计阻力，经2.5 s后落回手中，已知该星球半径为7220 km.
(1)该星球表面的重力加速度是多大？
(2)要使物体沿水平方向抛出而不落回星球表面，沿星球表面抛出的速度至少是多大？
(3)若物体距离星球无穷远处时其引力势能为零，则当物体距离星球球心r时其引力势能Ep＝－G
(式中m为物体的质量，M为星球的质量，G为引力常量)．问要使物体沿竖直方向抛出而不落回星球表面，沿星球表面抛出的速度至少是多大？