如图有两个转盘,每个转盘都分为3个相同大小的扇形区域,分别用序号1,2,3标出。现转动两个转盘,等转盘停止转动时, 指针指向每个区域的可能性相等(不计指针与两个区域交线重合的情形),将所得区域的序号相乘,比较所得积为奇数和偶数的概率的大小。有人说:因为两个转盘中奇数序号比偶数序号多,显然所得积为奇数的概率大,你同意他的说法吗?请说明理由。
指针指向每个区域的可能性相等(不计指针与两个区域交线重合的情形),将所得区域的序号相乘,比较所得积为奇数和偶数的概率的大小。有人说:因为两个转盘中奇数序号比偶数序号多,显然所得积为奇数的概率大,你同意他的说法吗?请说明理由。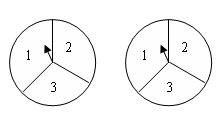
如图,CD切⊙于点D,连结OC,交⊙O于点B,过点B作弦AB⊥OD,点E为垂足,已知⊙O的半径为10。Sin∠COD= 。
。
求:①弦AB的长;
②阴影部分面积
在如图所示的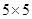 方格中,每个小正方形的边长都是
方格中,每个小正方形的边长都是 ,按下列要求画格点梯形(顶点都在格点上的梯形)并直接写出所画梯形的周长.
,按下列要求画格点梯形(顶点都在格点上的梯形)并直接写出所画梯形的周长.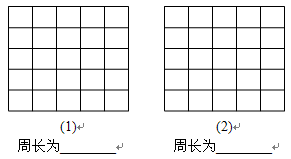
(1)在图1中画出一腰长为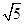 的梯形;
的梯形;
(2)在图2中画出一底边长为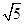 的梯形.
的梯形.
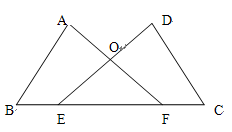
如图,点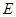 ,
, 在
在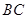 上,
上, 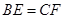 ,
,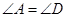 ,
,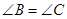 ,
,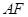 与
与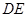 交于点
交于点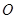 ,求证:
,求证: 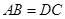
(1)计算: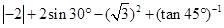
(2)先化简,再求值: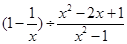 ,其中
,其中
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连结OA。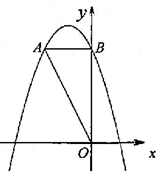
(1)求△OAB的面积;
(2)若抛物线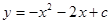 经过点A。
经过点A。
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可)。