已知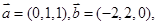 ,则向量
,则向量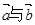 的夹角为
的夹角为
A. |
B. |
C. |
D.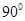 |
双曲线x2-y2=-3的( )
A.顶点坐标是(± ,0),虚轴端点坐标是(0,± ,0),虚轴端点坐标是(0,± ) ) |
B.顶点坐标是(0,± ),虚轴端点坐标是(± ),虚轴端点坐标是(± ,0) ,0) |
C.顶点坐标是(± ,0),渐近线方程是y=±x ,0),渐近线方程是y=±x |
D.虚轴端点坐标是(0,± ),渐近线方程是x=±y ),渐近线方程是x=±y |
设双曲线的两条准线把两焦点间的线段三等分,则此双曲线的离心率为( )
A. |
B. |
C. |
D.2 |
P为双曲线 -
- =1上的一点,F为一个焦点,以PF为直径的圆与圆x2+y2=a2的位置关系是( )
=1上的一点,F为一个焦点,以PF为直径的圆与圆x2+y2=a2的位置关系是( )
| A.内切 | B.内切或外切 | C.外切 | D.相离或相交 |
双曲线的两个焦点分别是(0,-5)、(0,5),离心率为1.5,则双曲线的方程为( )
A.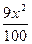 - - ="1" ="1" |
B. - - =1 =1 |
C. - - ="1" ="1" |
D. - -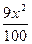 =1 =1 |
已知椭圆 +
+ =1和双曲线
=1和双曲线 -
- =1有公共的焦点,那么双曲线的渐近线方程是( )
=1有公共的焦点,那么双曲线的渐近线方程是( )
A.x=± y y |
B.y=± x x |
C.x=± y y |
D.y=± x x |