（本小题满分13分）
在一个盒子中，放有标号分别为2，3，4的三张卡片，现从
这个盒子中，有放回地先后抽得两张卡片的标号分别为ｘ，ｙ，记
．
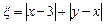(I)求随机变量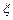
的最大值，并求事件“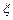取得最大值”的概率；
(Ⅱ)求随机变量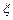的分布列和数学期望．
设椭圆C：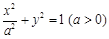
的两个焦点是
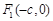和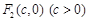
，且椭圆C与圆
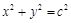有公共点，
（1）求a的取值范围；
（2）若椭圆上的点到焦点的最短距离为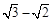
，求椭圆方程.
已知圆O：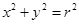
上的点到直线
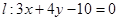的最小距离为1，设P为直线
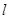上的点，过P点作圆O的两条切线PA、PB， 其中A、B为切点.
（1）求圆O的方程；
（2）当点P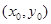
为直线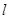上的定点时，求直线AB的方程.
已知函数
,x∈R.
（1）求函数
的最小正周期；
（2）求函数在区间
上的值域．
给定两个命题：
：对任意实数
都有
恒成立；
：关于的方程
有实数根；如果与中有且仅有一个为真命题，求实数
的取值范围．
一个袋子中装有质地均匀且完全相同的6个小球，其中黑球、白球各3个，
（1）从袋子中一次任取3个球，求3个小球颜色相同的概率；
（2）若取到1个黑球得1分，取到1个白球得2分，从袋子中取出1个小球记下得分后放入袋中，连续取球三次，求得分之和不小于4的概率.