如图7，利用一面墙（墙的最大可用长度为10米），用长为24米的篱笆围成中间隔有一道篱笆的长方形花圃ABCD．如果要在两个矩形的BC一边各开一个1.5米宽的门（做门材料不占用篱笆
），且花圃的总面积为54
平方米，那么花圃的宽AB应为多少米？
某车队要把4000吨货物运到雅安地震灾区（方案定后，每天的运量不变）。
（1）从运输开始，每天运输的货物吨数n（单位：吨）与运输时间t（单位：天）之间有怎样的函数关系式？
（2）因地震，到灾区的道路受阻，实际每天比原计划少运20%，则推迟1天完成任务，求原计划完成任务的天数。
如图，四边形ABCD中，AB∥CD，AC平分∠ABD，CE∥AD交AB于E．求证：四边形AECD是菱形；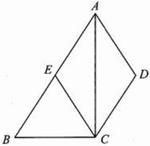
老师出了这样一道题：已知m=2015，求代数式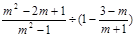
的值．小明不小心把2015看成了2014，但计算结果却和代入2014计算得出的结果一致，聪明的你，能说明其中的原因吗？试试看！
解方程：
（1）
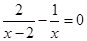（2）
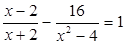
（3）．（2x+1）2-5=0（4）．（x－3）2＋2x（x－3）=0
计算或化简：
（1）计算：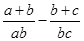
（2）计算：