设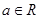 ,若函数
,若函数 ,
, 有大于
有大于 的极值点,则
的极值点,则
A.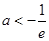 |
B.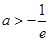 |
C.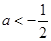 |
D. |
现有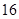 个不同小球,其中红色,黄色,蓝色,绿色小球各
个不同小球,其中红色,黄色,蓝色,绿色小球各 个,从中任取
个,从中任取 个,要求这
个,要求这 个小球不能是同一颜色,且红色小球至多
个小球不能是同一颜色,且红色小球至多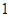 个,不同的取法为
个,不同的取法为
A. |
B.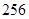 |
C. |
D. |
某企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了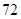 名员工进行调查,所得的数据如下表所示:
名员工进行调查,所得的数据如下表所示:
| 积极支持改革 |
不太支持改革 |
合计 |
|
| 工作积极 |
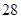 |
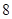 |
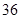 |
| 工作一般 |
 |
 [网] [网] |
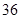 |
| 合计 |
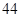 |
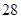 |
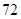 |
对于人力资源部的研究项目,根据上述数据能得出的结论是
(参考公式与数据: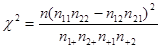 .当
.当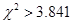 时,有
时,有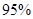 的把握说事件
的把握说事件 与
与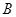 有关;当
有关;当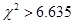 时,有
时,有 的把握说事件
的把握说事件 与
与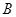 有关; 当
有关; 当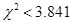 时认为事件
时认为事件 与
与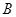 无关.)
无关.)
A.有 的把握说事件
的把握说事件 与
与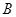 有关
有关
B.有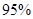 的把握说事件
的把握说事件 与
与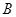 有关
有关
C.有 的把握说事件
的把握说事件 与
与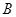 有关
有关
D.事件 与
与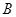 无关
无关
若 ,则
,则
A. |
B.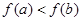 |
C. |
D.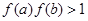 |
有一批产品,其中 件是正品,
件是正品, 件是次品,有放回的任取
件是次品,有放回的任取 件,若
件,若 表示取到次品的件数,则
表示取到次品的件数,则
A. |
B. |
C. |
D. |