两条平行直线上各有
个点，用这对点按如下的规则连接线段；
①平行线之间的点在连线段时，可以有共同的端点，但不能有其它交点；
②符合①要求的线段必须全部画出；
图1展示了当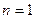
时的情况，此时图中三角形的个数为0；
图2展示了当
时的一种情况，此时图中三角形的个数为2；
（1）当
时，请在图3中画出使三角形个数最少的图形，此时图中有 个三角形；
（2）试猜想当对点时，按上述规则画出的图形中，最少有多少个三角形？此时最少三角形的个数能否为2010个？如果能为多少？ 
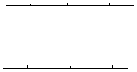
图1 图2 图3
如图，点O是△ABC外的一点，分别在射线OA，OB，OC上取点A′，B′，C′，使得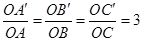
，连接A′B′，B′C′，C′A′，所得△A′B′C′与△ABC是否相似？证明你的结论．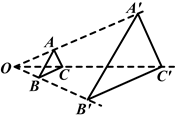
已知矩形ABCD的一条边AD＝8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．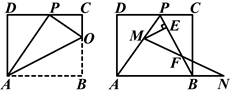
（1）如图1，已知折痕与边BC交于点O，连接AP、OP、OA．
①求证：△OCP∽△PDA；
②若△OCP与△PDA的面积比为1︰4，求边AB的长；
（2）若图1中的点P恰好是CD边的中点，求∠OAB的度数；
（3）如图2，在（1）的条件下，擦去折痕AO、线段OP，连接BP．动点M在线段AP上（点M与点P、A不重合），动点N在线段AB的延长线上，且BN＝PM，连接MN交PB于点F，作ME⊥BP于点E．试问当点M、N在移动过程中，线段EF的长度是否发生变化？若变化，说明理由；若不变，求出线段EF的长度．
为邓小平诞辰110周年献礼，广安市政府对城市建设进行了整改．如图，已知斜坡AB长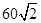
米，坡角（即∠BAC）为45°，BC⊥AC，现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE（下面两个小题结果都保留根号）．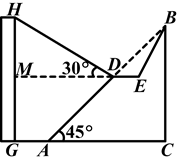
（1）若修建的斜坡BE的坡比为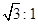
，求休闲平台DE的长是多少米；
（2）一座建筑物GH距离A点33米远（即AG＝33米），小亮在D点测得建筑物顶部H的仰角（即∠HDM）为30°．点B、C、A、G、H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？
如图，双曲线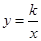
经过△OAB的顶点A和OB的中点C，AB∥x轴，点A的坐标为（2，3）．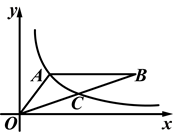
（1）确定k的值；
（2）若点D（3，m）在双曲线上，求直线AD的解析式；
（3）计算△OAB的面积．
如图，小明想测山高和索道的长度．他在B处仰望山顶A，测得仰角∠B＝31°，再往山的方向（水平方向）前进80m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE＝39°．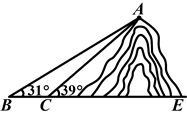
（1）求这座山的高度（小明的身高忽略不计）；
（2）求索道AC的长（结果精确到0.1m）．
（参考数据：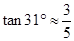
，
，
，
）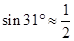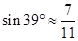