（本小题满分13分）
对于定义域为D的函数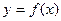
，若同时满足下列条件：
①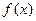
在D内单调递增或单调递减；②存在区间[
]
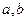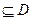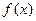，使在[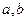]上的值域为[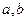]；那么把（
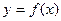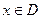）叫闭函数
（1）求闭函数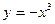
符合条件②
的区间[]；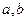
（2）判断函数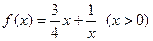
是否为闭函数？并说明理由；
（3）若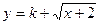
是闭函数，求实数
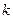的取值范围.
设关于x的函数y=2cos2x－2acosx－(2a+1)的最小值为f(a)，试确定满足f(a)=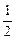
的a值，并对此时的a值求y的最大值.
设a>0,f(x)=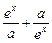
是R上的偶函数，(1)求a的值；(2)证明： f(x)在(0，+∞)上是增函数.
的偶函数，其图象关于点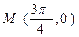
对称，且在区间
上是单调
函数.求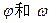
的值.
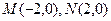已知两点
，点
为坐标平面内的动点，且满足
.
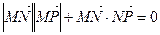(Ⅰ)求点的轨迹
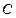的方程;
(Ⅱ)设过点
的直线
斜率为
，且与曲线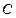相交于点
、
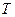，若、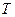两点只在第二象限内运动，线段
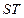的垂直平分线交
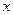轴于
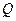点，求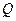点横坐标的取值范围.
已知函数
，直线
与函数
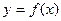图象相切.
（Ⅰ）求直线的斜率
的取值范围；
（Ⅱ）设函数
，已知函数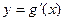
的图象经过点
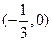，求函数
的极值.