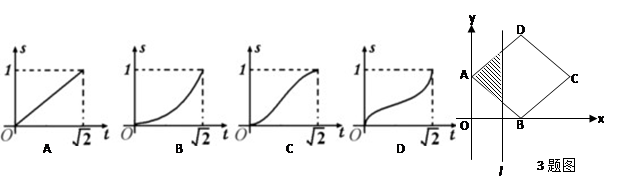设函数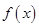 是定义在
是定义在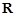 上的奇函数,且当
上的奇函数,且当 时,
时,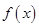 单调递减,若数列
单调递减,若数列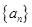 是等差数列,且
是等差数列,且 ,则
,则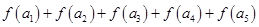 的值()
的值()
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
若函数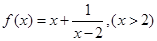 在
在 处有最小值,则
处有最小值,则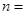 ( )
( )
A. |
B.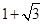 |
C.4 | D.3 |
右图是函数 在区间
在区间 上的图象。为了得到这个函数的图象,只要将
上的图象。为了得到这个函数的图象,只要将 的图象上所有的点()
的图象上所有的点()
A.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
B.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
已知 ,则 ( )
,则 ( )
A.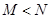 |
B.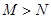 |
C.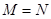 |
D.以上都有可能 |
如图,正方形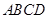 的顶点
的顶点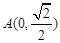 ,
,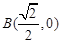 ,顶点
,顶点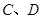 位于第一象限,直线
位于第一象限,直线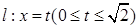 将正方形
将正方形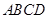 分成两部分,记位于直线
分成两部分,记位于直线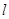 左侧阴影部分的面积为
左侧阴影部分的面积为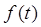 ,则函数
,则函数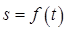 的图象大致是()
的图象大致是()