在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向外的匀强磁场,磁感应强度为B。一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示。不计粒子重 力,求:
力,求:
(1)M、N两点间的电势差UMN ;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从M点运动到P点的总时间t。
如图所示,水平地面上静止放置着物块B和C,相距l=1.0m。物块A以速度v0=10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度v=2.0m/s。已知A和B的质量均为 ,C的质量为A质量的K倍,物块与地面的动摩擦因数μ=0.45。(设碰撞时间很短,
,C的质量为A质量的K倍,物块与地面的动摩擦因数μ=0.45。(设碰撞时间很短,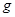 取10m/s2)
取10m/s2)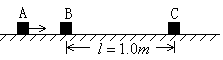
计算与C碰撞前瞬间AB的速度;
根据AB与C的碰撞过程分析K的取值范围,并讨论与C碰撞后AB的可能运动方向。
如图所示,在光滑的水平面上,有两个质量都是M的小车A和B,两车之间用轻质弹簧相连,它们以共同的速度v0向右运动,另有一质量为m =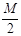 的粘性物体,从高处自由落下,正好落在A车上,并与之粘合在一起,求这以后的运动过程中,弹簧获得的最大弹性势能EP。
的粘性物体,从高处自由落下,正好落在A车上,并与之粘合在一起,求这以后的运动过程中,弹簧获得的最大弹性势能EP。
用中子轰击锂核(36Li)发生核反应,产生氚和α粒子并放出4.8 MeV的能量.写出核反应方程式;
求上述反应中的质量亏损为多少(保留两位有效数字);
若中子与锂核是以等大反向的动量相碰,则α粒子和氚的动能之比是多少?
某种金属光电效应过程中的极限频率8×1014Hz,已知h=6.63×10-34Js,求:该金属的逸出功多大?
当照射光的频率1×1015Hz时,从该金属表面逸出的光电子的最大初动能多大?
如图所示,真空室内竖直条形区域I存在垂直纸面向外的匀强磁场,条形
区域Ⅱ(含I、Ⅱ区域分界面)存在水平向右的匀强电场,电场强度为E,磁场和电场宽
度均为L且足够长,M、N为涂有荧光物质的竖直板。现有一束质子从A处连续不断地
射入磁场,入射方向与M板成60°夹角且与纸面平行如图,质子束由两部分组成,一部分为速度大小为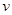 的低速质子,另一部分为速度大小为3
的低速质子,另一部分为速度大小为3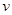 的高速质子,当I区中磁场较强时,M板出现两个亮斑,缓慢改变磁场强弱,直至亮斑相继刚好消失为止,此时观察到N板有两个亮斑。已知质子质量为m,电量为e,不计质子重力和相互作用力,求:
的高速质子,当I区中磁场较强时,M板出现两个亮斑,缓慢改变磁场强弱,直至亮斑相继刚好消失为止,此时观察到N板有两个亮斑。已知质子质量为m,电量为e,不计质子重力和相互作用力,求: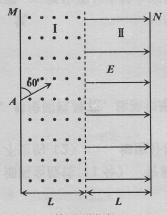
此时I区的磁感应强度;
N板两个亮斑之间的距离.